以下是小辰同学阅读的一份材料和思考：
五个边长为1的小正方形如图①放置，用两条线段把它们分割成三部分(如图②)，移动其中的两部分，与未移动的部分恰好拼接成一个无空隙无重叠的新正方形(如图③)．
小辰阅读后发现，拼接前后图形的面积相等，若设新的正方形的边长为x（x＞0），可得x2=5，x=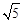
.由此可知新正方形边长等于两个小正方形组成的矩形的对角线长．
参考上面的材料和小辰的思考方法，解决问题：
五个边长为1的小正方形（如图④放置），用两条线段把它们分割成四部分，移动其中的两部分，与未移动的部分恰好拼接成一个无空隙无重叠的矩形，且所得矩形的邻边之比为1：2．
具体要求如下：
（1）设拼接后的长方形的长为a，宽为b，则a的长度为 ；
（2）在图④中，画出符合题意的两条分割线（只要画出一种即可）；
（3）在图⑤中，画出拼接后符合题意的长方形（只要画出一种即可）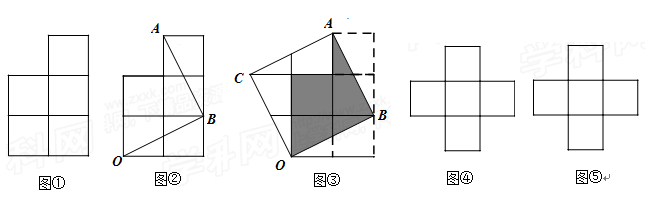
如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方
形的顶点上．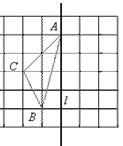 
（1）在图中画出与△ABC关于直线l成轴对称的△A′B′C′；
（2）在直线l上找一点P（在答题纸上图中标出），使PB+PC的长最短，这个最短长度是．
如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于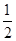
EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M，若CN⊥AM，垂足为N，求证：AN=MN．
如图，C为线段AB的中点，CD平分∠ACE，CE平分∠BCD，且CD＝CE，
求证：△ACD≌△BCE．
如图，已知：AB＝CB，AD＝CD，求证：∠A＝∠C．
数学实验室：（本题12分）
点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|．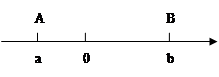
利用数形结合思想回答下列问题：
①数轴上表示2和5两点之间的距离是________,数轴上表示1和﹣3的两点之间的距离是________．(2分)
②数轴上表示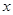
和
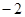的两点之间的距离表示为__________．(3分)
③若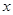表示一个有理数，且
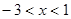，化简：
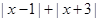(4分)
④若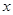表示一个有理数，且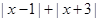＞4，则有理数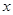的取值范围是___________________(3分)