某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.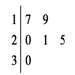
(1)若日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?
(2)从这6名工人中任取2人,设这两人加工零件的个数分别为 ,求
,求 的概率.
的概率.
已知梯形ABCD中,AB=DC=AD,AC和BD是它的对角线.用三段论证明:AC平分∠BCD,BD平分∠CBA.
把空间平行六面体与平面上的平行四边形类比,试由“平行四边形对边相等”得出平行六面体的相关性质.
已知函数f(x)= (x∈R),
(x∈R),
(1)判定函数f(x)的奇偶性;
(2)判定函数f(x)在R上的单调性,并证明.
如图1,若射线OM,ON上分别存在点M1,M2与点N1,N2,则 =
= ·
· ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
.已知f(x)= (x≠-
(x≠- ,a>0),且f(1)=log162,f(-2)=1.
,a>0),且f(1)=log162,f(-2)=1.
(1)求函数f(x)的表达式;
(2)已知数列{xn}的项满足xn=[1-f(1)][1-f(2)]…[1-f(n)],试求x1,x2,x3,x4;
(3)猜想{xn}的通项.