已知函数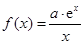 (
( ,
,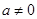 ).
).
(Ⅰ)当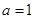 时,求曲线
时,求曲线 在点
在点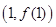 处切线的方程;
处切线的方程;
(Ⅱ)求函数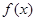 的单调区间;
的单调区间;
(Ⅲ)当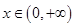 时,
时,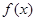
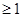 恒成立,求
恒成立,求 的取值范围.
的取值范围.
杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律。下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14个数与第15个数的比为 ,求n的值;
,求n的值;
(3)求n阶(包括0阶)杨辉三角的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35。显然,1+3+6+10+15=35。事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数。试用含有m、k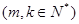 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。
经市场调查:生产某产品需投入年固定成本为3万元,每生产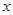 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,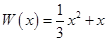 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时, (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量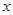 (万件)的函数解析式;
(万件)的函数解析式;
(注:年利润=年销售收入 固定成本
固定成本 流动成本)
流动成本)
(2)年产量为多少万件时,在这一商品的生产中所获利润最大?最大利润是多少?
设关于正整数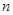 的函数
的函数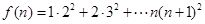
(1)求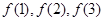 ;
;
(2)是否存在常数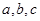 使得
使得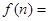
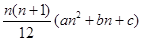 对一切自然数
对一切自然数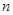 都成立?并证明你的结论
都成立?并证明你的结论
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是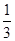 ,遇到红灯时停留的时间都是2 分钟. 设这名学生在路上遇到红灯的个数为变量
,遇到红灯时停留的时间都是2 分钟. 设这名学生在路上遇到红灯的个数为变量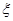 、停留的总时间为变量
、停留的总时间为变量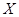 ,
,
(1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(2)这名学生在上学路上遇到红灯的个数至多是2个的概率.
(3)求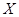 的标准差
的标准差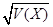 .
.
已知复数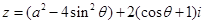 ,其中
,其中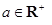 ,
,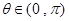 ,
,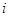 为虚数单位,且
为虚数单位,且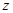 是方程
是方程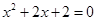 的一个根.
的一个根.
(1)求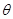 与
与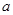 的值;
的值;
(2)若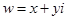 (
(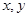 为实数),求满足
为实数),求满足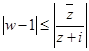 的点
的点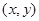 表示的图形的面积.
表示的图形的面积.