已知：函数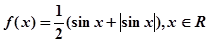
（1）求函数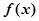
的周期T，与单调增区间.
（2）函数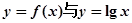
的图象有几个公共交点.
（3）设关于
的函数
的最小值为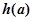
，试确定满足
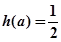的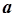
的值，并对此时的
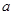值求
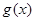的最小值．
如图，在某港口
处获悉，其正东方向20海里
处有一艘渔船遇险等待营救，此时救援船在港口的南偏西
据港口10海里的
处，救援船接到救援命令立即从处沿直线前往处营救渔船.
(Ⅰ) 求接到救援命令时救援船据渔船的距离；
（Ⅱ）试问救援船在处应朝北偏东多少度的方向沿直线前往处救援？（已知
）.
已知向量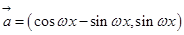
，
，设函数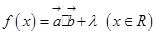
的图象关于直线
对称，其中
，
为常数，且
.
（Ⅰ）求函数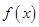
的最小正周期；
（Ⅱ）若
的图象经过点
，求函数在区间
上的取值范围.
在平面直角坐标系xOy中，曲线
与坐标轴的交点都在圆上．
（1）求圆C的方程；
（2）若圆C与直线
交于A，B两点，且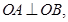
求a的值．
已知圆
和直线
(1) 求证:不论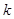
取什么值,直线和圆总相交;
(2) 求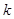取何值时,圆被直线截得的弦最短,并求最短弦的长.
已知一个圆C和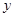
轴相切,圆心在直线
上,且在直线
上截得的弦长为
,求圆C的方程.