（本小题满分15分）如图所示,正方形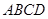
与直角梯形
所在平面互相垂直,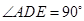
,
,
．
（1）求证：
平面
；
（2）求证：
平面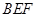
；
（3）求四面体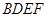
的体积．
（本小题满分14分）在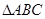
中,角
的对边分别为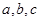
,已知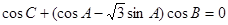
．
（Ⅰ）求角
的大小；
（Ⅱ）若
,求△
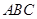的面积．
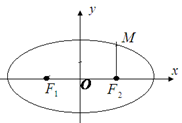
如图，已知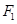
，
分别是椭圆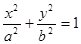
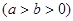的左、右焦点，过
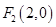与
轴垂直的直线交椭圆于点
，且
（1）求椭圆的标准方程；
（2）已知点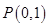
，问是否存在直线
与椭圆交于不同的两点
，
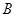，且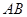
的垂直平分线恰好过
点？若存在，求出直线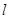斜率的取值范围；若不存在，请说明理由．
（原创）已知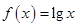
（1）若a>b>c>1，且a、b、c成等差数列，求证：
；
（2）若m>n>0时，有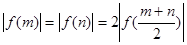
，求证：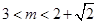
．
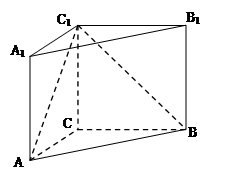
如图， 在直三棱柱
中，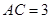
，
，
．
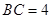（1）求证：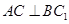
；
（2）问：是否在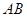
线段上存在一点
，使得
平面
？若存在，请证明；若不存在，请说明理由．
,
.
的最小正周期；
的取值范围.