如图示,摩托车做腾跃特技表演,以v0=10m/s的初速度冲上顶部水平的高台,然后从高台水平飞出,若摩托车冲向高台过程中以额定功率1.8kw行驶,所经时间为16s,人和车的总质量为180kg,台高h=6m,不计空气阻力,不计摩擦产生的热量(g取10m/s2)求:摩托车飞出的水平距离S是多少?
如图所示,倾角为30o的斜面B放在水平地面上,其上表面光滑,整体可以左右滑动。将小球A挂在倾角为θ的光滑斜面上,细绳方向与斜面平行。试求(要求细绳方向始终与斜面平行,g = 10m/s2):
(1)当斜面如何运动时,小球对斜面的压力为零。
(2)当斜面如何运动时,绳子的拉力为零.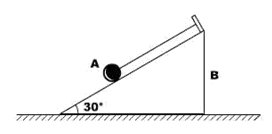
质量为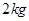 的物体在水平推力
的物体在水平推力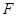 的作用下沿水平面作直线运动,运动6s后撤去
的作用下沿水平面作直线运动,运动6s后撤去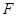 ,其运动的
,其运动的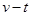 图像如图所示。
图像如图所示。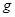 取10 m/s2,求:
取10 m/s2,求:
(1)6-10s内物体运动加速度的大小
(2)物体与水平面间的滑动摩擦力的大小
(3)水平推力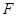 的大小
的大小
一带电粒子在xOy平面内运动,其轨迹如图所示,它从O点出发,以恒定的速率v沿y轴正方向射出,经一段时间到达P点. 图中x轴上方的轨迹都是半径为R的半圆,下方都是半径为r的半圆,不计重力的影响.
(1)如果此粒子带正电,且以上运动分别是在两个不同的匀强磁场中发生的,试判断磁场的方向,并求出这两个匀强磁场的磁感应强度的大小之比.
(2)求此粒子由O点到P点沿x轴方向运动的平均速度的大小.
如图所示,水平光滑地面上停放着一辆小车,左侧靠在竖直墙壁上,小车的四分之一圆弧轨道AB是光滑的,在最低点B与水平轨道BC相切,BC的长度是圆弧半径R的10倍,整个轨道处于同一竖直平面内。可视为质点的物块从A点正上方某处无初速下落,恰好落入小车圆弧轨道,然后沿水平轨道滑行至轨道末端C处恰好没有滑出。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍,小车的质量是物块的3倍,不考虑空气阻力和物块落入圆弧轨道时的能量损失。求: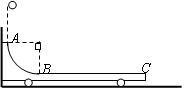
⑴物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍;
⑵物块与水平轨道BC间的动摩擦因数μ。
如图所示,一高空作业的工人质量为m=70kg,腰系一条安全带,若工人不慎跌落,当他的重心位置下降L=5m时,安全带呈竖直状态且开始绷直。已知安全带从开始绷直到拉伸至最长的缓冲时间为t=1.4s,求安全带受到的平均冲力是多大?(不计空气阻力,g取10m/s)