据环保部门测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比,比例常数为
 .现已知相距18
.现已知相距18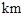 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设 (
(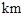 ).
).
(1)试将 表示为
表示为 的函数; (2)若
的函数; (2)若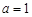 ,且
,且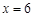 时,
时, 取得最小值,试求
取得最小值,试求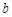 的值.
的值.
直线AB经过⊙O上的点C,并且OA=OB,CA=CB.⊙O交直线OB于E,D,连接EC,CD.
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED=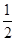 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
已知函数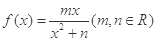 在
在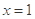 处取得极值
处取得极值 .
.
(1)求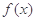 的表达式;
的表达式;
(2)设函数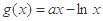 .若对于任意的
.若对于任意的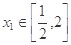 ,总存在唯一的
,总存在唯一的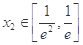 ,使得
,使得 ,求实数
,求实数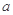 的取值范围.
的取值范围.
给定椭圆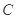 :
: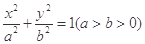 ,称圆心在原点
,称圆心在原点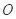 ,半径为
,半径为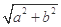 的圆是椭圆
的圆是椭圆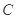 的“准圆”.若椭圆
的“准圆”.若椭圆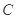 的一个焦点为
的一个焦点为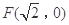 ,其短轴上的一个端点到
,其短轴上的一个端点到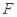 的距离为
的距离为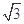 .
.
(1)求椭圆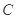 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点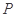 是椭圆
是椭圆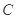 的“准圆”上的动点,过点
的“准圆”上的动点,过点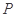 作椭圆的切线
作椭圆的切线 交“准圆”于点
交“准圆”于点 .
.
(ⅰ)当点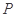 为“准圆”与
为“准圆”与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 的方程并证明
的方程并证明 ;
;
(ⅱ)求证:线段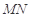 的长为定值.
的长为定值.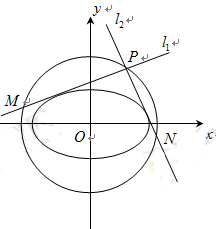
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
(1)试分别估计元件A、元件B为正品的概率;
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下;
(1)求生产5件元件B所获得的利润不少于300元的概率;
(2)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
如图,在直三棱柱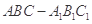 中,
中,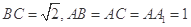 ,
, 是棱
是棱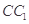 上的一点,
上的一点,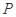 是
是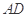 的延长线与
的延长线与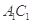 的延长线的交点,且
的延长线的交点,且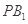 ∥平面
∥平面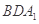 .
.
(1)求证: ;
;
(2)求二面角 的正弦值.
的正弦值.