已知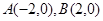 ,点
,点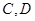 依次满足
依次满足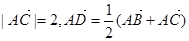 。
。
(1)求点 的轨迹;
的轨迹;
(2)过点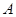 作直线
作直线 交以
交以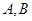 为焦点的椭圆于
为焦点的椭圆于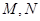 两点,线段
两点,线段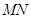 的中点到
的中点到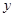 轴的距离为
轴的距离为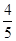 ,且直线
,且直线 与点
与点 的轨迹相切,求该椭圆的方程;
的轨迹相切,求该椭圆的方程;
(3)在(2)的条件下,设点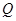 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点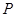 及以
及以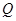 为圆心的一个圆,使得该圆与直线
为圆心的一个圆,使得该圆与直线 都相切,如存在,求出
都相切,如存在,求出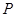 点坐标及圆的方程,如不存在,请说明理由.
点坐标及圆的方程,如不存在,请说明理由.
有粮食和石油两种物资,可用轮船与飞机两种方式运输,每天每艘轮船和每架飞机的运输效果见表.
 |
轮船运输量/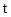 |
飞机运输量/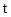 |
| 粮食 |
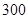 |
 |
| 石油 |
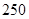 |
 |
现在要在一天内运输至少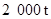 粮食和
粮食和 石油,需至少安排多少艘轮船和多少架飞机?
石油,需至少安排多少艘轮船和多少架飞机?
某运输公司接受了向抗洪救灾地区每天送至少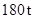 支援物资的任务.该公司有
支援物资的任务.该公司有 辆载重
辆载重 的
的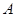 型卡车与
型卡车与 辆载重为
辆载重为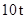 的
的 型卡车,有
型卡车,有 名驾驶员,每辆卡车每天往返的次数为
名驾驶员,每辆卡车每天往返的次数为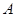 型卡车
型卡车 次,
次, 型卡车
型卡车 次;每辆卡车每天往返的成本费
次;每辆卡车每天往返的成本费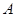 型为
型为 元,
元, 型为
型为 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排
元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排 型或
型或 型卡车,所花的成本费分别是多少?
型卡车,所花的成本费分别是多少?
已知实数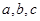 成等差数列,
成等差数列,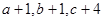 成等比数列,且
成等比数列,且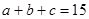 。
。
求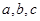 。
。
设等比数列 的前
的前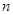 项和为
项和为 ,若
,若 ,求公比
,求公比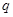 。
。
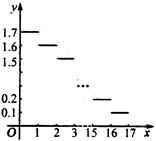
某同学要把自己的计算机接入因特网,现有两家ISP公司可供选择,公司A每小时受费1.5元;公司B的收费规则如下:在用户上网的第1小时内收费1.7元,第2小时内收费1.6元,以后每小时减少0.1元(若超过17小时,按17小时计算)如图所示.
假设一次上网时间总小于17小时,那么,一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少?请写出其中的不等关系.