已知椭圆 的左右焦点分别为
的左右焦点分别为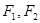 ,短轴两个端点为
,短轴两个端点为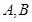 ,且四边形
,且四边形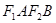 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若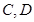 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点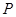 .证明:
.证明: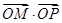 为定值;
为定值;
(3)在(2)的条件下,试问 轴上是否存在异于点
轴上是否存在异于点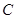 的定点
的定点 ,使得以
,使得以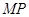 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点
的交点,若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.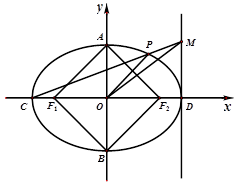
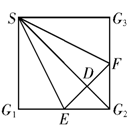
如图,正方形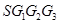 中,
中,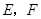 分别是
分别是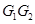 ,
, 的中点,
的中点,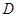 是
是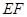 的中点,现沿
的中点,现沿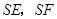 及
及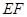 把这个正方形折成一个四面体,使
把这个正方形折成一个四面体,使 三点重合,重合后的点记为
三点重合,重合后的点记为 .
.
(1)求证:平面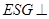 平面
平面 ;
;
(2)求二面角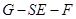 的余弦值.
的余弦值.
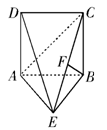
如图,直二面角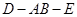 中,四边形
中,四边形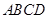 是边长为2的正方形,
是边长为2的正方形,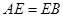 ,
,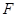 为
为 上的点,且
上的点,且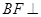 平面
平面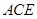 .
.
(1)求证: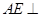 平面
平面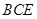 ;
;
(2)求二面角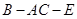 的大小;
的大小;
(3)求点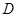 到平面
到平面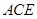 的距离.
的距离.
如图,已知正方体 的棱长为2,点
的棱长为2,点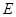 为棱
为棱 的中点.
的中点.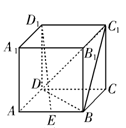
求:(1)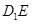 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(2)二面角 的余弦值.
的余弦值.
如图,底面是直角梯形的四棱锥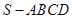 ,
,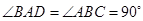 ,
,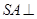 底面
底面 ,
, ,
,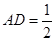 ,求面
,求面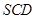 与面
与面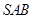 所成的二面角的余弦值.
所成的二面角的余弦值.
如图,在四棱锥 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 底面
底面 ,
,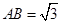 ,
, ,
, ,
, 为
为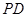 的中点.
的中点.
(1)求直线 与
与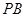 所成角的余弦值;
所成角的余弦值;
(2)在侧面 内找一点
内找一点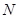 ,使
,使 面
面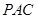 ,并求出
,并求出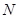 点到直线
点到直线 和
和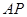 的距离.
的距离.