已知函数 .
.
(1)讨论函数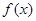 在
在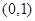 上的单调性;
上的单调性;
(2)当 时,曲线
时,曲线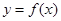 上总存在相异两点,
上总存在相异两点,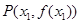 ,
, ,使得
,使得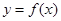 曲线在
曲线在 、
、 处的切线互相平行,求证:
处的切线互相平行,求证: .
.
(本小题满分12分)已知数列 的前项
的前项 和为
和为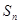 ,点
,点 均在函数
均在函数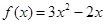 的图象上。
的图象上。
(1)求数列 的通项公式;
的通项公式;
(2)设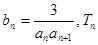 是数列
是数列 的前
的前 项和,求使得
项和,求使得 对所有
对所有 都成立的实数
都成立的实数 的范围.
的范围.
如图1在 中,
中,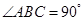 ,D、E分别为线段AB 、AC的中点,
,D、E分别为线段AB 、AC的中点, .以
.以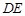 为折痕,将
为折痕,将 折起到图2的位置,使平面
折起到图2的位置,使平面 平面
平面 ,连接
,连接 ,设F是线段
,设F是线段 上的动点,满足
上的动点,满足 .
.

(1)证明:平面 ;
;
(2)若二面角 的大小为
的大小为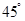 ,求
,求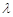 的值.
的值.
雅安市某中学随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].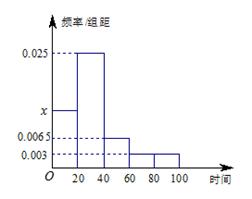
(1)求直方图中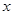 的值;
的值;
(2)如果上学路上所需时间不少于1小时的学生可申请在学校住宿,若招生1200名,请估计新生中有多少名学生可以申请住宿;
(3)从学校的高一学生中任选4名学生,这4名学生中上学路上所需时间少于20分钟的人数记为X,求X的分布列和数学期望.(以直方图中的频率作为概率)
已知向量 =(2sin x,
=(2sin x,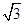 cos x),
cos x),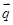 =(-sin x,2sin x),函数f(x)=
=(-sin x,2sin x),函数f(x)= ·
·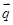
(1)求f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(C)=1,c=1,ab=2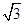 ,且a>b,求a,b的值.
,且a>b,求a,b的值.
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
我们把一系列向量 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作 ,已知向量列
,已知向量列 满足:
满足: ,
, 
 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)设 表示向量
表示向量 与
与 间的夹角,若
间的夹角,若 ,
, ,求
,求 ;
;
(3)设 ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.