某商店试销某种商品20天,获得如下数据:
| 日销售量(件) |
0 |
1 |
2 |
3 |
| 频数 |
1 |
5 |
9 |
5 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率。
(1)求当天商品不进货的概率;
(2)记
为第二天开始营业时该商品的件数,求
的分布列和数学期望。
焦点在x轴上的双曲线过点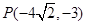 且点
且点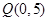 与两焦点的连线互相垂直。
与两焦点的连线互相垂直。
(1)求此双曲线的标准方程;
(2)过双曲线的右焦点倾斜角为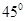 的直线与双曲线交于A、B两点,求
的直线与双曲线交于A、B两点,求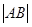 的长。
的长。
某高速公路某施工工地需调运建材100吨,可租用装载的卡车和农用车分别为10辆和20辆,若每辆卡车装载8吨,运费960元,每辆农用车装载2.5吨,运费360元,问两种车各租用多少辆时,才能一次性装完且总费用最低?
如图为函数y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,试求该函数的一个解析式.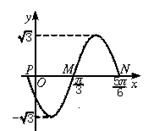
已知数列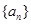 满足
满足 ,
,
(1)求 ;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和
;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和 。
。
若经过两点A(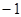 , 0),B(0, 2)的直线
, 0),B(0, 2)的直线 与圆
与圆 相切,求
相切,求 的值
的值