某高速公路某施工工地需调运建材100吨,可租用装载的卡车和农用车分别为10辆和20辆,若每辆卡车装载8吨,运费960元,每辆农用车装载2.5吨,运费360元,问两种车各租用多少辆时,才能一次性装完且总费用最低?
已知O(0,0)、A( ,0)为平面内两定点,动点P满足|PO|+|PA|=2.
,0)为平面内两定点,动点P满足|PO|+|PA|=2.
(I)求动点P的轨迹方程;
(II)设直线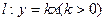 与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时
与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时
如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a.
(I)求证:AB1⊥BC1;
(II)求二面角B—AB1—C的大小;
(III)求点A1到平面AB1C的距离.
|
在△ABC中,三个内角是A、B、C的对边分别是a、b、c,其中c=10,且
 (I)求证:△ABC是直角三角形;
(I)求证:△ABC是直角三角形;
(II)设圆O过A、B、C三点,点P位于劣弧AC上,∠PAB=60°.求四边形ABCP的面积.
已知数列 是等差数列,其前n项和为
是等差数列,其前n项和为
(I)求数列 的通项公式;
的通项公式;
(II)设p、q是正整数,且p≠q.证明: .
.
(本小题满分15分)
已知函数 的图象在
的图象在 上连续不断,定义:
上连续不断,定义: 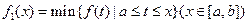 ,
,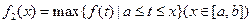
其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值, 表示函数
表示函数 在
在 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数 ,使得
,使得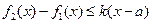 对任意的
对任意的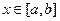 成立,则称函数
成立,则称函数 为
为 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(1)若 ,
, ,试写出
,试写出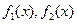 的表达式;
的表达式;
(2)已知函数 ,
,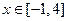 ,试判断
,试判断 是否为
是否为 上的“
上的“ 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知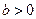 ,函数
,函数 是
是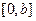 上的2阶收缩函数,求
上的2阶收缩函数,求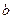 的取值范围.
的取值范围.