已知函数 ,
, ,且
,且 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)若函数 在区间
在区间 内有且仅有一个极值点,求
内有且仅有一个极值点,求 的取值范围;
的取值范围;
(3)设 为两曲线
为两曲线 ,
, 的交点,且两曲线在交点
的交点,且两曲线在交点 处的切线分别为
处的切线分别为 .若取
.若取 ,试判断当直线
,试判断当直线 与
与 轴围成等腰三角形时
轴围成等腰三角形时 值的个数并说明理由.
值的个数并说明理由.
已知抛物线 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于 轴(垂足为T),与抛物线交于不同的两点P、Q,且
轴(垂足为T),与抛物线交于不同的两点P、Q,且 .
.
(Ⅰ)求点T的横坐标 ;
;
(Ⅱ)若椭圆C以F1,F2为焦点,且F1,F2及椭圆短轴的一个端点围成的三角形面积为1.
① 求椭圆C的标准方程;
② 过点F2作直线l与椭圆C交于A,B两点,设 ,若
,若 的取值范围.
的取值范围.
已知函数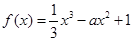
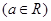 .
.
(Ⅰ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅱ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
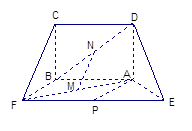
如图(1),在等腰梯形CDEF中,CB、DA是梯形的高,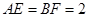 ,
,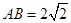 ,现将梯形沿CB、DA折起,使EF//AB且
,现将梯形沿CB、DA折起,使EF//AB且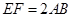 ,得一简单组合体
,得一简单组合体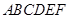 如图(2)所示,已知
如图(2)所示,已知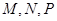 分别为
分别为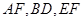 的中点.
的中点.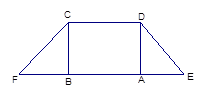
图(1) 图(2)
(Ⅰ)求证: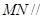 平面
平面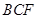 ;
;
(Ⅱ)求证: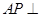 平面
平面 .
.
已知向量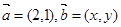
(Ⅰ)若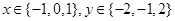 ,求向量
,求向量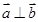 的概率;
的概率;
(Ⅱ)若用计算机产生的随机二元数组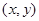 构成区域
构成区域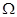 :
: ,求二元数组
,求二元数组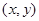 满足
满足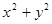
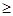 1的概率.
1的概率.
设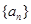 为等差数列,
为等差数列,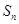 为数列
为数列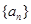 的前
的前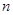 项和,已知
项和,已知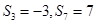 .
.
(Ⅰ)求数列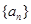 的通项公式;
的通项公式;
(Ⅱ)设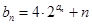 ,求数列
,求数列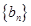 的前
的前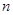 项和
项和 .
.