“光盘行动”倡导厉行节约,反对铺张浪费,带动大家珍惜粮食,吃光盘子中的食物,得到从中央到民众的支持,为了解某地响应“光盘行动”的实际情况,某校几位同学组成研究性学习小组,从某社区 岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
(1)求a,b的值,并估计本社区 岁的人群中“光盘族”所占比例;
岁的人群中“光盘族”所占比例;
(2)从年龄段在 的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
(1)已知选取2人中1人来自 中的前提下,求另一人来自年龄段
中的前提下,求另一人来自年龄段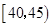 中的概率;
中的概率;
(2)求2名领队的年龄之和的期望值(每个年龄段以中间值计算).
(本小题满分16分)
已知数列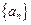 满足:
满足: ,
, ,
,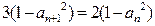 ,记数列
,记数列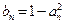 ,
,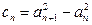 (
( ).
).
(1)证明数列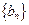 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在数列 的不同项
的不同项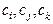 (
(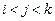 )使之成为等差数列?若存在请求出这样的不同项
)使之成为等差数列?若存在请求出这样的不同项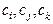 (
(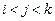 );若不存在,请说明理由.
);若不存在,请说明理由.
(本小题满分15分)
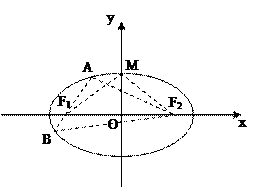
如图,椭圆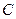 的中心在原点,焦点在
的中心在原点,焦点在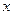 轴上,
轴上,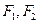 分别是椭圆
分别是椭圆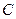 的左、右焦点,
的左、右焦点,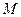 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过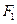 的直线
的直线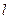 与椭圆交于
与椭圆交于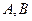 两点,
两点,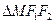 的面积为
的面积为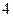 ,
,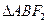 的周长为
的周长为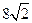 .
.
(1)求椭圆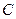 的方程;
的方程;
(2)设点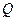 的坐标为
的坐标为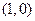 ,是否存在椭圆上的点
,是否存在椭圆上的点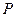 及以
及以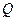 为圆心的一个圆,使得该圆与直线
为圆心的一个圆,使得该圆与直线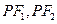 都相切,如存在,求出
都相切,如存在,求出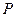 点坐标及圆的方程,如不存在,请说明理由.
点坐标及圆的方程,如不存在,请说明理由.
(本小题满分15分)
某企业有两个生产车间分别在A,B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A,B,C中任意两点间的距离均有1 km,设∠BDC=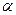 ,所有员工从车间到食堂步行的总路程为S.
,所有员工从车间到食堂步行的总路程为S.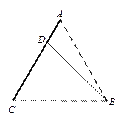
(1)写出S关于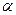 的函数表达式,并指出
的函数表达式,并指出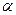 的取值范围;
的取值范围;
(2)问食堂D建在距离A多远时,可使总路程S最少?
(本小题满分14分)
如图,四棱锥P-ABCD中,底面ABCD为菱形,且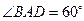 ,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.
,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.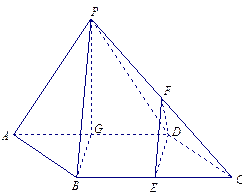
(1)求证:BG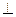 面PAD;
面PAD;
(2)E是BC的中点,在PC上求一点F,使得PG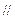 面DEF.
面DEF.
(本小题满分14分)
设已知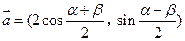 ,
,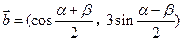 ,其中
,其中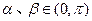 .
.
(1)若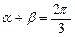 ,且
,且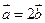 ,求
,求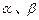 的值;
的值;
(2)若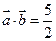 ,求
,求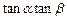 的值.
的值.