(本小题满分16分)
已知数列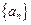 满足:
满足: ,
, ,
,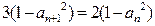 ,记数列
,记数列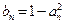 ,
,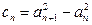 (
( ).
).
(1)证明数列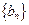 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在数列 的不同项
的不同项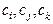 (
(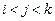 )使之成为等差数列?若存在请求出这样的不同项
)使之成为等差数列?若存在请求出这样的不同项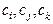 (
(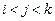 );若不存在,请说明理由.
);若不存在,请说明理由.
已知椭圆C: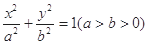 ,⊙
,⊙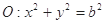 , 点
, 点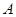 ,
,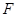 分别是椭圆
分别是椭圆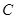 的左顶点和左焦点,点
的左顶点和左焦点,点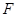 不是
不是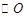 上的点,点
上的点,点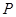 是
是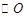 上的动点.
上的动点.
(1)若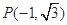 ,
,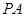 是
是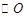 的切线,求椭圆
的切线,求椭圆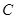 的方程;
的方程;
(2)是否存在这样的椭圆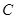 ,使得
,使得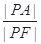 恒为常数?如果存在,求出这个数及
恒为常数?如果存在,求出这个数及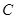 的离心率
的离心率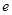 ;如果不存在,说明理由.
;如果不存在,说明理由.
在如图所示的几何体中, 是边长为2的正三角形,
是边长为2的正三角形,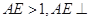 平面
平面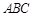 ,
,
平面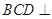 平面
平面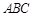 ,
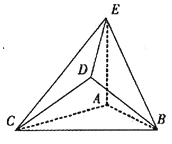
,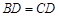 ,且
,且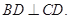
(1)若 ,求证:
,求证: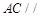 平面
平面
(2)若二面角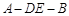 为60°,求
为60°,求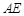 的长.
的长.
某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年增加2万元,从第八年开始,每年的维护费用比上年增加25%
(1)设第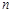 年该生产线的维护费用为
年该生产线的维护费用为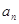 ,求
,求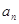 的表达式;
的表达式;
(2)若该生产线前 年每年的平均维护费用大于12万元时,需要更新生产线,求该生产线前
年每年的平均维护费用大于12万元时,需要更新生产线,求该生产线前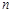 年每年的平均维护费用,并判断第几年年初需要更新该生产线?
年每年的平均维护费用,并判断第几年年初需要更新该生产线?
已知函数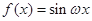
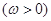 在区间
在区间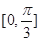 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形 中,
中,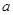 ,
,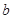 ,
,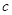 为
为 的内角
的内角 的对边,且满足
的对边,且满足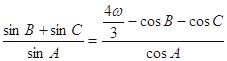 .
.
(1)证明:
(2)若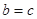 ,
, ,
, ,
, ,求四边形
,求四边形 面积的最大值.
面积的最大值.
已知函数 .
.
(Ⅰ)当 时,求
时,求 的单调区间
的单调区间
(Ⅱ)若不等式 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;
(Ⅲ)定义:对于函数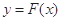 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数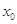 ,称
,称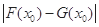 的值为两函数在
的值为两函数在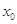 处的差值。证明:当
处的差值。证明:当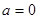 时,函数
时,函数 和
和 在其公共定义域内的所有差值都大干2.
在其公共定义域内的所有差值都大干2.