已知椭圆C: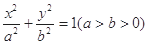 ,⊙
,⊙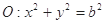 , 点
, 点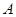 ,
,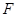 分别是椭圆
分别是椭圆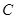 的左顶点和左焦点,点
的左顶点和左焦点,点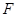 不是
不是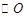 上的点,点
上的点,点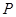 是
是 上的动点.
上的动点.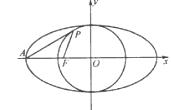
(1)若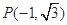 ,
,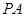 是
是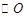 的切线,求椭圆
的切线,求椭圆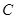 的方程;
的方程;
(2)是否存在这样的椭圆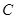 ,使得
,使得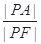 恒为常数?如果存在,求出这个数及
恒为常数?如果存在,求出这个数及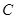 的离心率
的离心率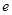 ;如果不存在,说明理由.
;如果不存在,说明理由.
(本小题满分12分)(注意:在试题卷上作答无效)
已知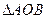 的顶点A在射线
的顶点A在射线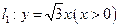 上,
上,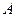 、
、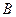 两点关于x轴对称,0为坐标原点,
两点关于x轴对称,0为坐标原点,
且线段AB上有一点M满足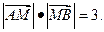 当点A在
当点A在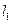 上移动时,记点M的轨迹为W.
上移动时,记点M的轨迹为W.
(Ⅰ)求轨迹W的方程;
(Ⅱ)设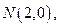 是否存在过
是否存在过 的直线
的直线 与W相交于P,Q两点,使得
与W相交于P,Q两点,使得 若存在,
若存在,
求出直线 ;若不存在,说明理由.
;若不存在,说明理由.
本小题满分12分)(注意:在试题卷上作答无效)
设数列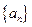 的前n项和为
的前n项和为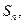 已知
已知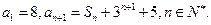
(Ⅰ)设 证明:数列
证明:数列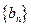 是等比数列;
是等比数列;
(Ⅱ)证明: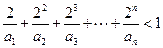 .
.
(本小题满分12分)(注意:在试题卷上作答无效)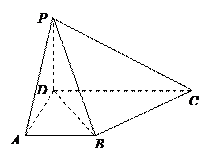
在四棱锥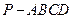 中,侧面
中,侧面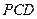
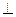 底面
底面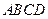 ,
,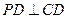 ,底面
,底面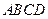 是直角梯形,
是直角梯形,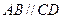 ,
,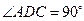 ,
,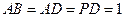 ,
,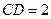 .
.
(Ⅰ)求证: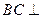 平面
平面 ;
;
(Ⅱ)设 为侧棱
为侧棱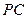 上一点,
上一点,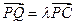 ,
,
试确定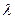 的值,使得二面角
的值,使得二面角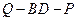 为
为 .
.
本小题满分12分)(注意:在试题卷上作答无效)
在进行一项掷骰子放球的游戏中规定:若掷出1点或2点,则在甲盒中放一球;否则,在乙盒中放一球。现在前后一共掷了4次骰子,设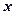 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。
(Ⅰ)求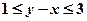 的概率;
的概率;
(Ⅱ)若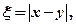 求随机变量
求随机变量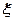 的分布列和数学期望。
的分布列和数学期望。
(本小题满分10分)(注意:在试题卷上作答无效) 的三个内角A,B,C所对的边分别为a,b,c, 向量
的三个内角A,B,C所对的边分别为a,b,c, 向量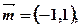
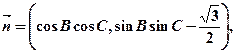 且
且
(Ⅰ)求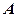 的大小;
的大小;
(Ⅱ)现给出下列四个条件:①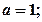 ②
② ③
③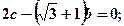 ④
④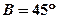 .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 ,求出你所确定的
,求出你所确定的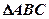 的面积.
的面积.