四个小动物换座位，开始是鼠、猴、兔、猫分别坐1、2、3、4号位上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，…这样交替进行下去，那么第202次互换座位后，小兔坐在第（）号座位上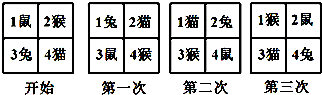
| A．1 | B．2 | C．3 | D．4 |
已知[x]表示不超过实数x的最大整数（x∈R），如：[﹣1.3]=﹣2，[0.8]=0，[3.4]=3．定义{x}=x﹣[x]，求{
}+{
}+{
}+…+{
}=（）
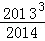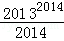| A．1006 | B．1007 | C．1008 | D．2014 |
在实数集R中定义一种运算“⊕”，具有性质：
①对∀a，b∈R，a⊕b=b⊕a；
②对∀a∈R，a⊕0=a；
③对∀a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c；
那么函数f（x）=x⊕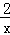
（x≥1）的最小值为（）
| A．5 | B．4 | C．2+2 |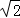
D．2 |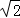
若函数y=f（x）满足：集合A={f（n）|n∈N*}中至少有三个不同的数成等差数列，则称函数f（x）是“等差源函数”，则下列四个函数中，“等差源函数”的个数是（）
①y=2x+1；
②y=log2x；
③y=2x+1；
④y=sin（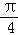
x+）
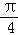| A．1 | B．2 | C．3 | D．4 |
定义一种新运算：a⊗b=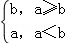
，已知函数f（x）=（1+
）⊗3log2（x+1），若方程f（x）﹣k=0恰有两个不相等的实根，则实数k的取值范围为（）
| A．（﹣∞，3） |
| B．（1，3） |
| C．（﹣∞，﹣3）∪（1，3） |
| D．（﹣∞，﹣3）∪（0，3） |
则函数
的零点个数是( )