设函数f(x)=a·b,其中向量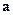
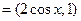 ,向量
,向量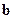
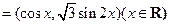 .
.
(1)求f(x)的最小正周期;
(2)在∆ABC中,a,b,c分别是角A,B,C的对边,f(A)=2,a= ,b+c=3,求b,c的长.
,b+c=3,求b,c的长.
过抛物线y2=4x的焦点F作倾斜角为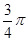 的直线,它与抛物线交于A、B两点,求这两点间的距离.
的直线,它与抛物线交于A、B两点,求这两点间的距离.
已知直线l经过点P(1,1),倾斜角为 ,且tan
,且tan =
=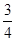
(1)写出直线l的一个参数方程;
(2)设l与圆x2+y2=4相交于两点A,B,求点P到A,B两点的距离之积.
(普通班做)圆O1和圆O2的极坐标方程分别为ρ=4cosθ,ρ=-sinθ.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过圆O1,圆O2两个交点的直线的直角坐标方程.
设进入某商场的每一位顾客购买甲种商品的概率为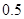 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记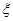 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求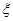 的分布列及期望。
的分布列及期望。
某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
画出上表数据的散点图为: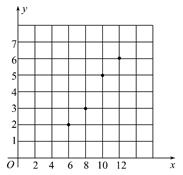
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程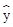 =
=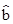 x+
x+ .
.
(2)试根据(1)求出的线性回归方程,预测记忆力为9的学生的判断力
( 其中 ,
,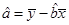 )
)