已知{an}是一个公差大于0的等差数列，且满足a4a5=55,a3+a6=16
（1）求数列{an}的通项公式；
（2）若数列{an}和数列{bn}满足等式：
an-1=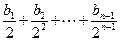
，an=
（
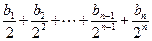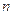为正整数），
设数列{bn}的前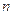项和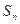
，cn=(an+19)(Sn+50),数列{cn}前n项和为Tn，
求Tn的最小值
如图，四棱锥
中，底面
为平行四边形，
底面
（1）证明：平面
平面
;
（2）若二面角
大小为
，求
与平面
所成角的正弦值.
某市教育局为了了解高三学生体育达标情况，在某学校的高三学生体育达标成绩中随机抽取100个进行调研，按成绩分组：第l组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]得到的频率分布直方图如图所示：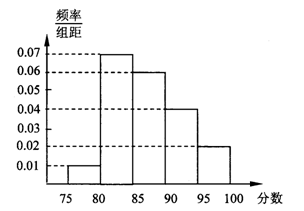
若要在成绩较高的第3，4，5组中用分层抽样抽取6名学生进行复查：
（1）已知学生甲和学生乙的成绩均在第四组，求学生甲和学生乙至少有一人被选中复查的概率；
（2）在已抽取到的6名学生中随机抽取3名学生接受篮球项目的考核，设第三组中有三名学生接受篮球项目的考核，求暑的分布列和数学期望．
已知函数
相邻两个对称轴之间的距离是
，且满足，
（1）求
的单调递减区间；
（2）在钝角△ABC中，a、b、c分别为角A、B、C的对边，sinB=
,求△ABC的面积。
设不等式
的解集为M，
.
（1）证明：
；
（2）比较
与
的大小，并说明理由.
已知曲线
的直角坐标方程为
. 以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系. P是曲线上一点，
，
，将点P绕点O逆时针旋转角
后得到点Q，
，点M的轨迹是曲线
.
（1）求曲线的极坐标方程；
（2）求
的取值范围.