设数列{an}满足a1＝2，a2＋a4＝8，且对任意n∈N*，函数f(x)＝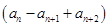
x＋an＋1cos x－an＋2sin x满足f′
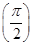＝0．
(1)求数列{an}的通项公式；
(2)若bn＝2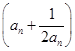
，求数列{bn}的前n项和Sn．
.椭圆
＞
＞
与直线
交于
、
两点，且
，其
中
为坐标原点。
1）求
的值；
2）若椭圆的离心率
满足
，求椭圆长轴的取值范围。
.．(满分12分)
已知二次函数
的图像经过坐标原点，其导函数为
，数列
的前
项和为
，点
均在函数的图像上。
1）求数列的通项公式；
2）设
，
是数列
的前项和，求使得
对所有
都成立的最小正整数
。
. (满分12分
)定义在
上的函数
满足
，且
，当
时，
。1）求在
上的解析式；
2）若在
上是减函数，求函数在上的值域。
(满分12分) 在
中，
分别是角
的对边，且
。
1）求
的大小；
2）若
，
，求的面积。
本大题9分）
已知与圆C：
相切的直线l分别交x轴和y轴正半轴于A，B两点，O为原点，且|OA|=a，|OB|=b（a＞2，b＞2）。
（1）求证：（a-2）（b-2）=2；
（2）求△AOB面积的最小值。