已知数列{an}的前n项和Sn=-an- n-1+2(n∈N*),数列{bn}满足bn=2nan.
n-1+2(n∈N*),数列{bn}满足bn=2nan.
(1)求证数列{bn}是等差数列,并求数列{an}的通项公式.
(2)设数列 的前n项和为Tn,证明:n∈N*且n≥3时,Tn>
的前n项和为Tn,证明:n∈N*且n≥3时,Tn>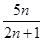 .
.
(3)设数列{cn}满足an(cn-3n)=(-1)n-1λn(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有cn+1>cn.
设函数 .
.
(1)求 的值域;
的值域;
(2)记△ABC的内角A,B,C的对边长分别为a,b,c,若 ,求a的值.
,求a的值.
定义:若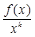 在
在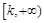 上为增函数,则称
上为增函数,则称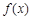 为“k次比增函数”,其中
为“k次比增函数”,其中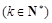 . 已知
. 已知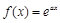 其中e为自然对数的底数.
其中e为自然对数的底数.
(1)若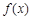 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;
(2)当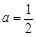 时,求函数
时,求函数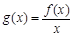 在
在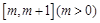 上的最小值;
上的最小值;
(3)求证: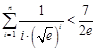 .
.
已知椭圆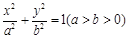 的离心率
的离心率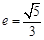 ,且直线
,且直线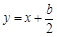 是抛物线
是抛物线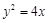 的一条切线.
的一条切线.
(1)求椭圆的方程;
(2)点P 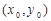 为椭圆上一点,直线
为椭圆上一点,直线 ,判断l与椭圆的位置关系并给出理由;
,判断l与椭圆的位置关系并给出理由;
(3)过椭圆上一点P作椭圆的切线交直线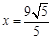 于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线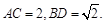 AE、CF都与平面ABCD垂直,AE=1,CF=2.
AE、CF都与平面ABCD垂直,AE=1,CF=2.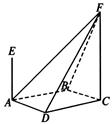
(1)求二面角B-AF-D的大小;
(2)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
“根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.”某市交警在该市一交通岗前设点对过往的车辆进行抽查,经过一晚的抽查,共查出酒后驾车者60名,图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图.
(1)统计方法中,同一组数据常用该组区间的中点值作为代表,图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计,求出图乙输出的S的值,并说明S的统计意义;(图乙中数据 与
与 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率) 
(2)本次行动中,吴、李两位先生都被酒精测试仪测得酒精浓度属于70~90 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90 范围的酒后驾车者中随机抽出2人抽血检验,设
范围的酒后驾车者中随机抽出2人抽血检验,设 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求 的分布列,并求吴、李两位先生至少有1人被抽中的概率;
的分布列,并求吴、李两位先生至少有1人被抽中的概率;