如图,在三棱锥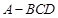 中,
中, ,
, ,
,
设顶点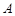 在底面
在底面 上的射影为
上的射影为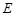 .
.
(Ⅰ)求证: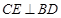 ;
;
(Ⅱ)设点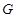 在棱
在棱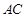 上,且
上,且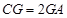 ,
,
试求二面角 的余弦值
的余弦值 
(本小题满分12分)
先阅读以下不等式的证明,再类比解决后面的问题
若 ,则
,则 .
.
证明:构造二次函数
将 展开得:
展开得:

 对一切实数
对一切实数 恒有
恒有 ,且抛物线的开口向上
,且抛物线的开口向上 ,
, .
.
(Ⅰ)类比猜想:
若 ,则 .
,则 .
(在横线上填写你的猜想结论)
(Ⅱ)证明你的猜想结论.
(本小题满分12分)
在 中,已知
中,已知 ,且
,且 .
.
(Ⅰ)求 的大小。
的大小。
(Ⅱ)证明 是等边三角形
是等边三角形
k
(本小题满分14分)
设动圆 过点
过点 ,且与定圆
,且与定圆
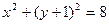 内切,动圆圆心
内切,动圆圆心 的轨迹记为曲线
的轨迹记为曲线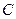 ,点
,点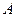 的坐标为
的坐标为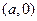 .
.
(1)求曲线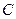 的方程;
的方程;
(2)若点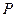 为曲线
为曲线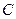 上任意一点,求点
上任意一点,求点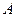 和点
和点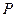 的距离的最大值
的距离的最大值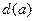 ;
;
(3)当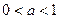 时,在(2)的条件下,设
时,在(2)的条件下,设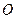 是坐标原点,
是坐标原点,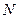 是曲线
是曲线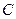 上横坐标为
上横坐标为 的点,记△
的点,记△ 的面积为
的面积为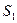 ,以
,以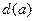 为边长的正方形的面积为
为边长的正方形的面积为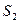 .若正数
.若正数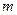 满足
满足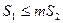 ,问
,问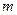 是否存在最小值?若存在,求出此最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出此最小值;若不存在,请说明理由.
(本小题满分14分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(1)求实数a的取值范围;
(2)设 ,
, 的导数为
的导数为 ,令
,令
求证: .
.
(本小题满分14分)
设等差数列 前
前 项和为
项和为 ,则有以下性质:
,则有以下性质: 成等差数列.
成等差数列.
(1) 类比等差数列的上述性质,写出等比数列 前
前 项积
项积 的类似性质;
的类似性质;
(2) 证明(1)中所得结论.