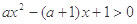（本小题满分14分）
已知函数
，
为实数）有极值，且在
处的切线与直线
平行.
（1）求实数a的取值范围；
（2）设
，
的导数为
，令
求证：
.
（本题12分）设等差数列第10项为24，第25项为-21
（1）求这个数列的通项公式；（2）设为其前n项和，求使取最大值时的n值。
（本题12分）建造一个容积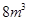为
，深为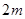
的长方体无盖水池，如果池底和池壁的造价分别为每平方米120元和80元，那么水池的最低总造价是多少元？
（1）以下是计算
的程序框图，请写出对应的程序
解：对应的程序如下: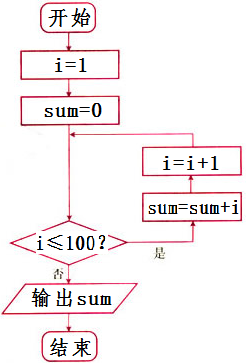
（2）二进数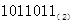
化为8进制数
已知26辆货车以相同速度v由A地驶向400千米处的B地，每两辆货车间距离为d千米，现已知d与v的平方成正比，且当v=20（千米／时）时，d=1（千米）．
（1）写出d与v的函数关系；
（2）若不计货车的长度，则26辆货车都到达B地最少需要多少小时？此时货车速度是多少？
解关于x的不等式