某造纸厂拟建一座底面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/平方米,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16米,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价.
已知一个三角形的三边边长分别为 ,设计一个算法,求出它的面积。
,设计一个算法,求出它的面积。
已知 .
.
求证:当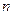 为偶数时,
为偶数时,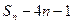 能被
能被 整除.
整除.
求证:(1)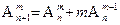
(2)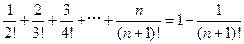
在二项式(axm+bxn)12(a>0,b>0,m、n≠0)中有2m+n=0,如果它的展开式里最大系数项恰是常数项.(1)求它是第几项(2)求 的范围.
的范围.
(满分14分)一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
(1)如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
(2)如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
|