如图,在四棱锥A—BCC1B1中,等边三角形ABC所在平面与正方形BCC1B1所在平面互相垂直,D为CC1的中点.
(1)求证:BD⊥AB1;
(2)求二面角B—AD—B1的余弦值.
(本小题满分10分)如图,在长方体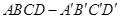 中,
中,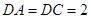 ,
,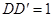 ,
, 与
与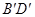 相交于点
相交于点 ,点
,点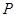 在线段
在线段 上(点
上(点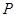 与点
与点 不重合).
不重合).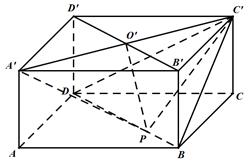
(1)若异面直线 与
与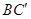 所成角的余弦值为
所成角的余弦值为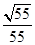 ,求
,求 的长度;
的长度;
(2)若 ,求平面
,求平面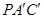 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分10分,不等式选讲)
已知正实数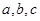 满足
满足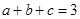 ,求证:
,求证: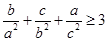 .
.
(本小题满分10分,矩阵与变换)
已知矩阵 ,
,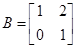 ,若矩阵
,若矩阵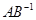 对应的变换把直线
对应的变换把直线 变为直线
变为直线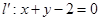 ,求直线
,求直线 的方程.
的方程.
(本小题满分10分,几何证明选讲)
如图, 与圆
与圆 相切于点
相切于点 ,
, 是
是 的中点,过点
的中点,过点 引圆
引圆 的割线,与圆
的割线,与圆 相交于点
相交于点 ,连结
,连结 .
.
求证: .
.
已知函数 ,
, .
.
(1)若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若直线 是函数
是函数 图象的切线,求
图象的切线,求 的最小值;
的最小值;
(3)当 时,若
时,若 与
与 的图象有两个交点
的图象有两个交点 ,求证:
,求证:
 .
.
(取 为
为 ,取
,取 为
为 ,取
,取 为
为 )
)