为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图: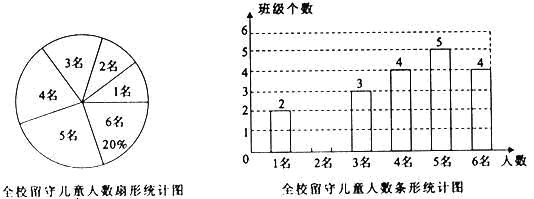
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
五子棋深受广大棋友的喜爱.规则是:10×10的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上首先连成五颗者为胜.如图是小张和小王的对弈图(小张执黑子先行,小王执白子后走).
观察棋盘思考:若A点的位置记作(8,4),小张必须在哪个位置上落子才不会让小王在短时间内获胜?为什么?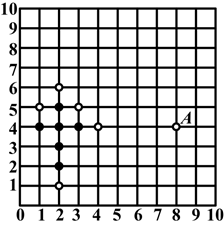
已知,点A(-2,3)、B(4,3)、C(-1,-3).
(1)求A、B两点之间的距离.
(2)求点C到x轴的距离.
(3)求△ABC的面积.
(4)观察线段AB与x轴的关系,若点D是线段AB上一点,则点D的纵坐标有什么特点?
有序数对(m,n)中的整数m,n满足m-n=-6,且点P(m,n)在第二象限,写出所有符合条件的数对.
如图所示的平面直角坐标系中,写出点A,B,C,D,E,F,O各点的坐标.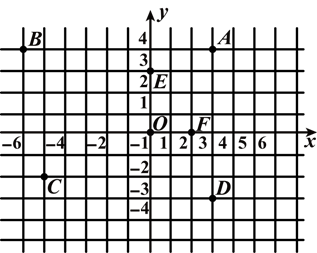
国际象棋、中国象棋和围棋号称世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置;
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).