如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.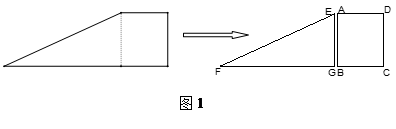
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。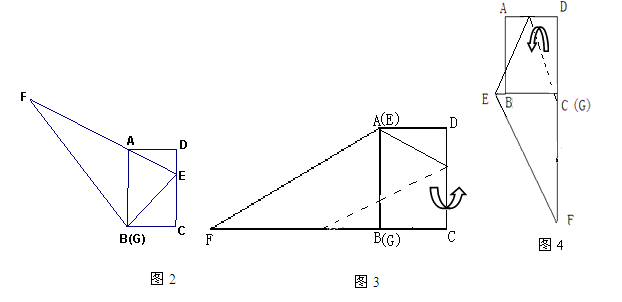
如图,已知∠A=∠C,∠1+∠2=180°,试问:∠B与∠F有什么关系?为什么?
解:∠B=∠F,理由如下:
∵∠A=∠C
∴∥()
∴∠BDC=∠B()
∵∠1+∠2=180°
且∠1+∠3()
∴∠3+∠2=180°
∴∥()
∴∠BDC=()
∴∠B=∠F()
如图所示,某校一块长为2a米的正方形空地是七年级4个班的清洁区,其中分给七(1)班的清洁区是一块边长为 米的正方形,
米的正方形, 。
。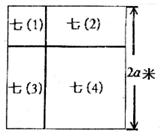
(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米?
已知∠1=∠2=∠3=59°,求∠4的度数。
先化简,再求值: ,其中
,其中
计算
(1)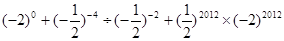
(2)