如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.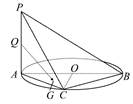
(1)求证:平面PAC⊥平面PBC.
(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
设函数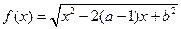 的定义域为
的定义域为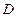 .
.
(I)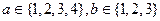 ,求使
,求使 的概率;
的概率;
(II) ,求使
,求使 的概率.
的概率.
已知△ 的周长为
的周长为 ,且
,且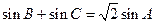 .
.
(1)求边长 的值;
的值;
(2)若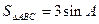 ,求
,求 的正切值.
的正切值.
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数 的分布列与期望.
的分布列与期望.
已知向量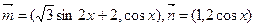 ,设函数
,设函数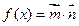 。
。
(1)求 的最小正周期与单调递减区间
的最小正周期与单调递减区间
(2)在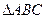 中,
中, 、
、 、
、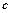 分别是角
分别是角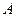 、
、 、
、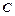 的对边,若
的对边,若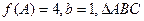 的面积为
的面积为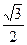 ,求
,求 的值。
的值。
数列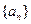 的各项均为正数,
的各项均为正数,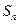 为其前
为其前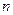 项和,对于任意
项和,对于任意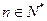 ,总有
,总有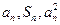 成等差数列.
成等差数列.
(1)求数列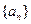 的通项公式;
的通项公式;
(2)设数列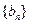 的前
的前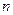 项和为
项和为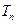 ,且
,且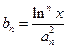 ,求证:对任意实数
,求证:对任意实数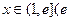 是常数,
是常数, 和任意正整数
和任意正整数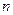 ,总有
,总有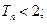
(3)正数数列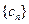 中,
中,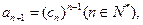 求数列
求数列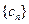 中的最大项.
中的最大项.