数列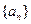 的各项均为正数,
的各项均为正数,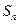 为其前
为其前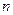 项和,对于任意
项和,对于任意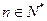 ,总有
,总有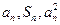 成等差数列.
成等差数列.
(1)求数列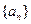 的通项公式;
的通项公式;
(2)设数列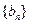 的前
的前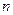 项和为
项和为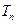 ,且
,且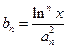 ,求证:对任意实数
,求证:对任意实数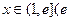 是常数,
是常数, 和任意正整数
和任意正整数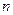 ,总有
,总有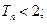
(3)正数数列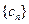 中,
中,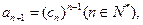 求数列
求数列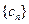 中的最大项.
中的最大项.
设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,  sin2x),x∈R.
sin2x),x∈R.
(Ⅰ)若f(x)=1- 且x∈[-
且x∈[- ,
, ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量c=(m,n)(|m|< )平移后得到函数y=f(x)的图象,求实数m、n的值。
)平移后得到函数y=f(x)的图象,求实数m、n的值。
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:5,6,7,8,9,10。把这6名学生的得分看成一个总体。(1)求该总体的平均数;(2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本。求该样本平均数与总体平均数之差的绝对值不超过0.5的概率。
已知向量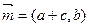 ,
,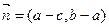 ,且
,且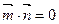 ,其中A、B、C是
,其中A、B、C是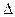 ABC的内角,
ABC的内角,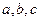 分别是角A,B,C的对边。
分别是角A,B,C的对边。
(Ⅰ)求角C的大小;
(Ⅱ)求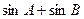 的取值范围;
的取值范围;
对于定义在区间D上的函数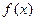 ,若存在闭区间
,若存在闭区间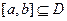 和常数
和常数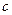 ,使得对任意
,使得对任意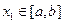 ,都有
,都有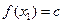 ,且对任意
,且对任意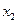 ∈D,当
∈D,当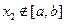 时,
时,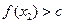 恒成立,则称函数
恒成立,则称函数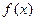 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数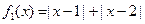 和
和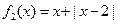 是否为R上的“平底型”函数?并说明理由;
是否为R上的“平底型”函数?并说明理由;
(Ⅱ)设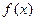 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式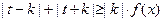 对一切
对一切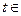 R恒成立,求实数
R恒成立,求实数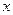 的取值范围;
的取值范围;
(Ⅲ)若函数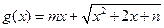 是区间
是区间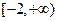 上的“平底型”函数,求
上的“平底型”函数,求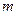 和
和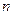 的值.
的值.
已知椭圆中心在原点,焦点在y轴上,离心率为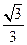 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线 相切.
相切.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设点F是椭圆在y轴正半轴上的一个焦点,点A,B是抛物线 上的两个动点,且满足
上的两个动点,且满足 ,过点A,B分别作抛物线的两条切线,设两切线的交点为M,试推断
,过点A,B分别作抛物线的两条切线,设两切线的交点为M,试推断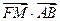 是否为定值?若是,求出这个定值;若不是,说明理由.
是否为定值?若是,求出这个定值;若不是,说明理由.