已知椭圆中心在原点，焦点在y轴上，离心率为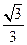
，以原点为圆心，椭圆短半轴长为半径的圆与直线
相切.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设点F是椭圆在y轴正半轴上的一个焦点，点A，B是抛物线
上的两个动点，且满足
，过点A，B分别作抛物线的两条切线，设两切线的交点为M，试推断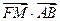
是否为定值？若是，求出这个定值；若不是，说明理由.
已知函数
．
（I）当
时，求
的最大值和最小值；
（II）设
的内角
所对的边分别为
，且
，若向量
与向量
共线，求
的值．
已知数列
，满足
（I）求证：数列
均为等比数列；
（Ⅱ）求数列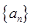
的通项公式
；
（Ⅲ）求证：
．
以点F1（－1,0），F2（1,0）为焦点的椭圆C经过点（1，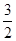
）。
（I）求椭圆C的方程；
（II）过P点分别以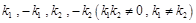
为斜率的直线分别交椭圆C于A，B，M，N，求证： 
使得
如图，PDCE为矩形，ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD＝∠ADC＝90°，AB＝AD＝
CD＝1，PD＝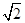
。
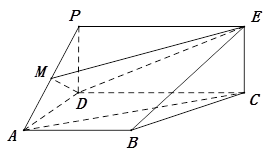
（I）若M为PA中点，求证：AC∥平面MDE；
（II）求直线PA与平面PBC所成角的正弦值；
（III）在线段PC上是否存在一点Q（除去端点），使得平面QAD与平面PBC所成锐二面角的大小为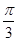
？
已知函数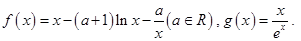
（I）求f（x）的单调区间；
（II）当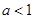
时，若存在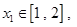
使得对任意的
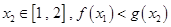恒成立，求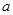
的取值范围。