为了降低能源损耗，某体育馆的外墙需要建造隔热层．体育馆要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度
（单位：cm）满足关系：
(
，
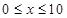为常数)，若不建隔热层，每年能源消耗费用为8万元．设
为隔热层建造费用与20年的能源消耗费用之和．
（1）求的值及的表达式；
（2）隔热层修建多厚时，总费用达到最小？并求最小值．
（本小题满分12分）
某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查，发现：
①销售数量y1（万件）与时间（月份）具有满足下表的一次函数关系：
| 时间x（月份） |
1 |
2 |
3 |
… |
11 |
12 |
| 销售数量y1（万件） |
1.7 |
1.8 |
1.9 |
… |
2.7 |
2.8 |
②每一件的销售利润y2与时间x（月份）具有如下图所示的关系。
请根据以上信息解答下列问题：
(Ⅰ)在三月份，销售这种商品可获利润多少万元？
(Ⅱ)哪一个月的销售利润最大？请说明理由。
（本小题满分12分）
函数
的图象关于
对称，当
时
；
（Ⅰ）写出的解析式并作出图象；
（Ⅱ）根据图象讨论
（
）的根的情况.
（本小题满分12分）
某简谐运动得到形如
的关系式，其中：振幅为4，周期为6
，初相为
；
（Ⅰ）写出这个确定的关系式；
（Ⅱ）用五点作图法作出这个函数在一个周期内的图象.
（本小题满分12分）
已知a=（1,2）,b=（-3,1）.
(Ⅰ) 求a－2b；
(Ⅱ) 设a, b的夹角为
,求
的值;
(Ⅲ)若向量a＋kb与a－kb互相垂直，求
的值.
计算下列各题（本小题满分12分）
（1）
；
（2）
；
（3） 