已知 是复数,
是复数, 和
和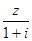 均为实数.
均为实数.
(1)求复数 ;
;
(2)若复数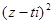 在复平面内对应点在第一象限,求实数t的取值范围.
在复平面内对应点在第一象限,求实数t的取值范围.
(本小题满分14分)
如图, 在四棱锥 中,顶点
中,顶点 在底面
在底面 上的射影恰好落在
上的射影恰好落在 的中点
的中点 上,又∠
上,又∠ ,
, ,且
,且
=1:2:2.
(1) 求证: 
(2) 若 , 求直线
, 求直线 与
与 所成的角的余弦值;
所成的角的余弦值;
(3) 若平面 与平面
与平面 所成的角为
所成的角为 , 求
, 求 的值
的值
(本小题满分14分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.
三人各向目标射击一次,求至少有一人命中目标的概率;
三人各向目标射击一次,求恰有两人命中目标的概率;
(3)若甲单独向目标射击三次,求他恰好命中两次的概率.
(本小题满分14分)
已知数列{ }是首项为
}是首项为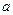 等于1且公比
等于1且公比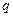 不等于1的等比数列,
不等于1的等比数列,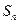 是其前
是其前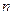 项的和,
项的和,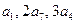 成等差数列.
成等差数列.
(1) 求和 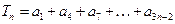 ;
;
(2) 证明 12 成等比数列
成等比数列
(本小题满分14分)
已知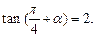
(1)求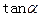 的值
的值
(2)求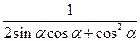 的值
的值
(本小题满分14分)
某造船公司年最高造船量是20艘. 已知造船x艘的产值函数为R(x)="3700x" + 45x2 – 10x3(单位:万元), 成本函数为C (x) =" 460x" + 5000 (单位:万元). 又在经济学中,函数f(x)的边际函数Mf (x)定义为: Mf (x) =" f" (x+1) – f (x). 求:
(1) 利润函数P(x) 及边际利润函数MP(x);
(2) 年造船量安排多少艘时, 可使公司造船的年利润最大?
(3) 边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?