在平面直角坐标系中,已知椭圆.如图所示,斜率为且不过原点的直线交椭圆于,两点,线段的中点为,射线交椭圆于点,交直线于点.
(1)求的最小值;
(2)若
(i)求证:直线过定点;
(ii)试问点能否关于轴对称?若能,求出此时的外接圆方程;若不能,请说明理由.

已知直线方程为 ,其中
,其中
(1)求证:直线恒过定点;
(2)当 变化时,求点
变化时,求点 到直线的距离的最大值;
到直线的距离的最大值;
(3)若直线分别与 轴、
轴、 轴的负半轴交于
轴的负半轴交于 两点,求
两点,求 面积的最小值及此时的直线方程.
面积的最小值及此时的直线方程.
在△ 中,
中, 所对的边分别为
所对的边分别为 ,
, ,
, .
.
(1)求 ;
;
(2)若 ,求
,求 .21世纪教育
.21世纪教育
设公差不为0的等差数列 的首项为1,且
的首项为1,且 构成等比数列.
构成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 …
… 1-
1- ,n∈N*,求
,n∈N*,求 的前n项和
的前n项和 .
.
已知关于 的不等式
的不等式 的解集为
的解集为 .
.
(1)求实数 的值;
的值;
(2)解关于 的不等式:
的不等式: (
( 为常数).
为常数).
设 ,
, 是函数
是函数 的图象上任意两点,若
的图象上任意两点,若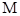 为
为 ,
, 的中点,且
的中点,且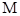 的横坐标为
的横坐标为 .
.
(1)求 ;
;
(2)若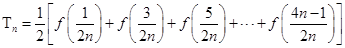 ,
, ,求
,求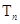 ;
;
(3)已知数列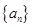 的通项公式
的通项公式 (
( ,
, ),数列
),数列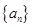 的前
的前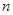 项和为
项和为 ,若不等式
,若不等式 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.