已知 是椭圆
是椭圆 上一点,且点
上一点,且点 到椭圆的两个焦点距离之和为
到椭圆的两个焦点距离之和为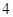 ;
;
(1)求椭圆方程;
(2)设 为椭圆的左顶点,直线
为椭圆的左顶点,直线 交
交 轴于点
轴于点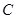 ,过
,过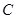 作斜率为
作斜率为 的直线
的直线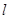 交椭圆于
交椭圆于 两点,若
两点,若 ,求实数
,求实数 的值.
的值.
已知双曲线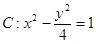 ,
,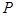 为
为 上任意一点;
上任意一点;
(1)求证:点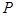 到双曲线
到双曲线 的两条渐近线的距离的乘积是一个常数;
的两条渐近线的距离的乘积是一个常数;
(2)设点 ,求
,求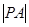 的最小值.
的最小值.
已知圆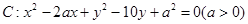 截直线
截直线 的弦长为
的弦长为 ;
;
(1)求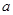 的值;
的值;
(2)求过点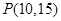 的圆的切线所在的直线方程.
的圆的切线所在的直线方程.
已知抛物线 ,过点
,过点
 作直线
作直线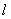 交抛物线于
交抛物线于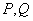 (点
(点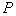 在第一象限);
在第一象限);
(1)设点 关于
关于 轴的对称点为
轴的对称点为 ,直线
,直线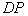 交
交 轴于点
轴于点 ,求证:
,求证: 为定点;
为定点;
(2)若 ,
, 为抛物线
为抛物线 上的三点,且
上的三点,且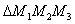 的重心为
的重心为 ,求线段
,求线段 所在直线的斜率的取值范围.
所在直线的斜率的取值范围.
已知抛物线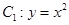 ,
,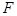 为抛物线的焦点,椭圆
为抛物线的焦点,椭圆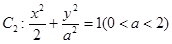 ;
;
(1)若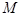 是
是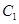 与
与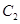 在第一象限的交点,且
在第一象限的交点,且 ,求实数
,求实数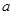 的值;
的值;
(2)设直线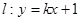 与抛物线
与抛物线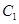 交于
交于 两个不同的点,
两个不同的点, 与椭圆
与椭圆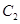 交于
交于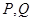 两个
两个
不同点,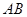 中点为
中点为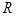 ,
, 中点为
中点为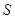 ,若
,若 在以
在以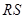 为直径的圆上,且
为直径的圆上,且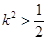 ,求实数
,求实数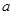
的取值范围.