如图,长方体中,,,点,分别在 上,过点,的平面与此长方体的面相交,交线围成一个正方形.

(Ⅰ)在图中画出这个正方形(不必说明画法与理由);
(Ⅱ)求平面把该长方体分成的两部分体积的比值.
(本小题满分12分)如图,在平面直角坐标系 中,点
中,点 在单位圆
在单位圆 上,
上, ,且
,且 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 也是单位圆
也是单位圆 上的点,且
上的点,且 .过点
.过点 分别做
分别做 轴的垂线,垂足为
轴的垂线,垂足为 ,记
,记 的面积为
的面积为 ,
, 的面积为
的面积为 .设
.设 ,求函数
,求函数 的最大值.
的最大值.
(本小题满分10分)已知集合 ,
, .
.
(1)分别求 ,
, ;
;
(2)已知集合 ,若
,若 ,求实数
,求实数 的取值集合.
的取值集合.
(本小题满分12分)已知函数 (
( ),
), .
.
(Ⅰ)求证: 在区间
在区间 上单调递增;
上单调递增;
(Ⅱ)若 ,函数
,函数 在区间
在区间 上的最大值为
上的最大值为 ,求
,求 的解析式,并判断
的解析式,并判断 是否有最大值和最小值,请说明理由(参考数据:
是否有最大值和最小值,请说明理由(参考数据: )
)
如图,O为坐标原点,点F为抛物线C1: 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2: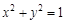 相切于点Q.
相切于点Q.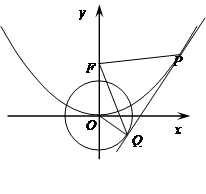
(Ⅰ)当直线PQ的方程为 时,求抛物线C1的方程;
时,求抛物线C1的方程;
(Ⅱ)当正数 变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求
变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求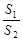 的最小值.
的最小值.
(本小题满分12分)如图,在三棱台 中,
中, 分别为
分别为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若 平面
平面 ,
,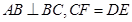 ,
, ,求平面
,求平面 与平面
与平面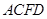 所成角(锐角)的大小.
所成角(锐角)的大小.