已知 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求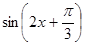 的值.
的值.
已知函数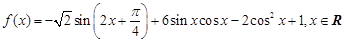 .
.
(Ⅰ)求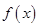 的最小正周期;
的最小正周期;
(Ⅱ)求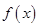 在区间
在区间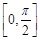 上的最大值和最小值.
上的最大值和最小值.
甲、乙两人参加某种选拔测试.在备选的 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是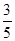 ,乙能答对其中的
,乙能答对其中的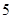 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的 道题中随机抽出
道题中随机抽出 道题进行测试,答对一题加
道题进行测试,答对一题加 分,答错一题(不答视为答错)减
分,答错一题(不答视为答错)减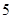 分,至少得
分,至少得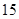 分才能入选.
分才能入选.
(Ⅰ)求乙的得分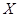 的分布列和数学期望
的分布列和数学期望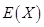 ;
;
(Ⅱ)求甲、乙两人中至少有一人入选的概率.
(本小题14分)已知函数 在其定义域上满足:
在其定义域上满足: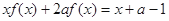 ,
,
(1)函数 的图象是否是中学对称图形?若是,请指出其对称中心(不证明)
的图象是否是中学对称图形?若是,请指出其对称中心(不证明)
(2)当 时,求
时,求 的取值范围
的取值范围
(3)若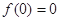 ,数列
,数列 满足
满足 ,那么若
,那么若 正整数N满足n>N时,对所有适合上述条件的数列
正整数N满足n>N时,对所有适合上述条件的数列 ,
,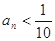 恒成立,求最小的N.
恒成立,求最小的N.
(1)(本小题6分)在平面直角坐标系中,已知某点 ,直线
,直线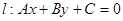 .求证:点P到直线
.求证:点P到直线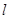 的距离
的距离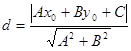
(2)(本小题7分)已知抛物线C: 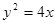 的焦点为F,点P(2,0),O为坐标原点,过P的直线
的焦点为F,点P(2,0),O为坐标原点,过P的直线 与抛物线C相交于A,B两点,若向量
与抛物线C相交于A,B两点,若向量 在向量
在向量 上的投影为n,且
上的投影为n,且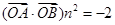 ,求直线
,求直线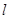 的方程.
的方程.