(本小题满分13分)甲、乙、丙三人参加某次招聘会,若甲应聘成功的概率为 ,乙、丙应聘成功的概率均为
,乙、丙应聘成功的概率均为 ,且三人是否应聘成功是相互独立的.
,且三人是否应聘成功是相互独立的.
(Ⅰ)若甲、乙、丙都应聘成功的概率是 ,求
,求 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,设 表示甲、乙两人中被聘用的人数,求
表示甲、乙两人中被聘用的人数,求 的数学期望.
的数学期望.
小李、小王、小张三人在一起做游戏时,需要确定做游戏的先后顺序,他们约定用“剪刀、布、锤子”的方式确定,在一个回合中.求:
(Ⅰ) 恰有一人出“布”的概率;
(Ⅱ) 至少有一人出“布”的概率.
已知函数 ,满足:①对任意
,满足:①对任意 ,都有
,都有
 ;
;
②对任意n∈N *都有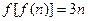 .
.
(Ⅰ)试证明: 为
为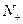 上的单调增函数;
上的单调增函数;
(Ⅱ)求 ;
;
(Ⅲ)令 ,试证明:
,试证明:
函数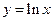 关于直线
关于直线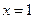 对称的函数为
对称的函数为 ,又函数
,又函数 的导函数为
的导函数为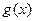 ,记
,记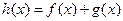 .
.
(Ⅰ)设曲线 在点
在点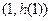 处的切线为
处的切线为 ,
,  与圆
与圆 相切,求
相切,求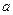 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)求函数 在[0,1]上的最大值.
在[0,1]上的最大值.
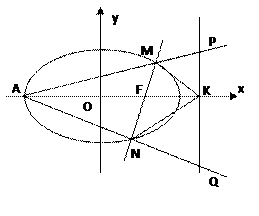 如图,已知椭圆
如图,已知椭圆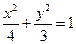 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.
(Ⅰ)求证:KF平分∠MKN;
(Ⅱ)直线AM、AN分别交准线 于点P、Q,
于点P、Q,
设直线MN的倾斜角为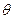 ,试用
,试用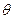 表示
表示
线段PQ的长度|PQ|,并求|PQ|的最小值.
(本小题满分13分)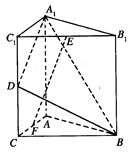 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求A1B与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B-A1D-A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.