(本小题满分13分)如图1,直角梯形 中,
中, ,
, ,
, .
. 交
交 于点
于点 ,点
,点 ,
, 分别在线段
分别在线段 ,
, 上,且
上,且 .将图1中的
.将图1中的 沿
沿 翻折,使平面
翻折,使平面 ⊥平面
⊥平面 (如图2所示),连结
(如图2所示),连结 、
、 ,
, 、
、 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)当三棱锥 的体积最大时,求直线
的体积最大时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(选修4-1 几何证明选讲)
如图,已知:C是以AB为直径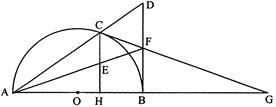 的半圆O上一点,
的半圆O上一点,
CH⊥AB于点H,直线AC与过B点的切线相交于
点D,E为CH中点,连接AE并延长交BD于点F,
直线CF交直线AB于点G.
(Ⅰ)求证:F是BD的中点;
(Ⅱ)求证:CG是⊙O的切线.
( 本题满分16满分)已知函数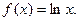 (1)求证:当
(1)求证:当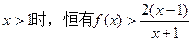 ;(2)求证:当
;(2)求证:当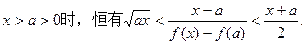
(本题满分16满分)设正项数列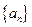 的前
的前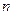 项和为
项和为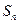 ,
,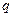 为非零常数.已知对任意正整数
为非零常数.已知对任意正整数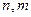 ,当
,当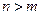 时,
时,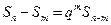 总成立.
总成立.
(1)证明:数列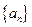 是等比数列;(2)若正整数
是等比数列;(2)若正整数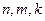 成等差数列,求证:
成等差数列,求证: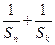 ≥
≥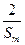 .
.
(本题满分16满分)设A、B分别为椭圆 (a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.
(a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.
已知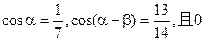 <
<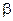 <
< <
<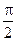 ,
,
(Ⅰ)求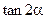 的值.(Ⅱ)求
的值.(Ⅱ)求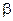 .
.