已知函数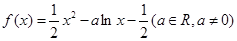 .
.
(1)当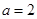 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 的单调区间;
的单调区间;
(3)若对任意的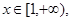 都有
都有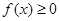 恒成立,求实数
恒成立,求实数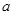 的取值范围.
的取值范围.
已知二次函数 (
( )
)
(1)若方程 有两个相等的实数根,求
有两个相等的实数根,求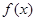 的解析式;
的解析式;
(2)若函数 在区间
在区间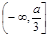 内单调递减,求a的取值范围
内单调递减,求a的取值范围
已知椭圆E的中心在原点,焦点在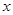 轴上,椭圆上的点到两个焦点的距离之和为
轴上,椭圆上的点到两个焦点的距离之和为 ,离心率
,离心率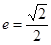
(1)求椭圆E的方程;
(2)作直线l: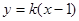 交椭圆E于点P、Q,且OP^OQ。求实数k的值.
交椭圆E于点P、Q,且OP^OQ。求实数k的值.
已知数列{an}的前n项和为Sn, ,满足
,满足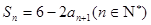 ,
,
(1)求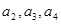 的值;
的值;
(2)猜想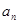 的表达式。
的表达式。
已知二次函数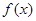 的二次项系数为a,且不等式f(x)>-2x的解集为(-1,3)。
的二次项系数为a,且不等式f(x)>-2x的解集为(-1,3)。
(1)若方程 有两个相等的实数根,求
有两个相等的实数根,求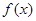 的解析式;
的解析式;
(2)若函数 在区间
在区间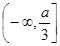 内单调递减,求a的取值范围;
内单调递减,求a的取值范围;
在三棱锥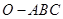 中,
中,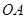 、
、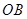 、
、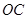 两两垂直,且
两两垂直,且 ,
, ,点
,点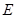 是棱
是棱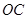 的中点.
的中点.
(1)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)求二面角 的余弦值.
的余弦值.