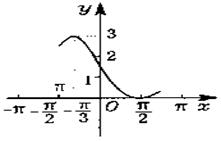
如图所示,某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料,已知已有两面墙 、
、 的夹角为
的夹角为 (即
(即 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 米),为了使得仓库的面积尽可能大,记
米),为了使得仓库的面积尽可能大,记 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 
设复数z=(m2+2m-3)+(m-1)i, 试求m取何值时
(1)Z是实数;
(2)Z是纯虚数;
(3)Z对应的点位于复平面的第一象限.
(本小题满分13分)在平面直角坐标系中,已知三个点的坐标分别为: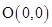 ,
,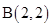 ,
,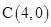 .
.
(1)若过点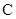 作一条直线
作一条直线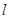 ,使点
,使点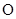 和点
和点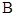 到直线
到直线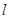 的距离相等,求直线
的距离相等,求直线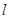 的方程;
的方程;
(2)求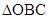 的外接圆的方程.
的外接圆的方程.
(本小题满分15分)如图,正方形 的边长为1,正方形
的边长为1,正方形 所在平面与平面
所在平面与平面 互相垂直,
互相垂直, 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
(1)利用“五点法”画出函数 在长度为一个周期的闭区间的简图
在长度为一个周期的闭区间的简图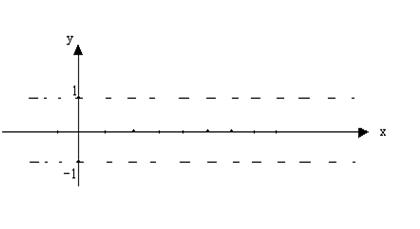
(2)并说明该函数图象可由y=sinx(x R)的图象经过怎样平移和伸缩变换得到的。
R)的图象经过怎样平移和伸缩变换得到的。
.已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图)所示.
①求函数的解析式;②求这个函数的单调区间.