如果数列
同时满足：（1）各项均不为
，（2）存在常数k, 对任意
都成立，则称这样的数列为“类等比数列” .由此等比数列必定是“类等比数列” .问：
（1）各项均不为0的等差数列
是否为“类等比数列”？说明理由.
（2）若数列为“类等比数列”，且
(a，b为常数)，是否存在常数λ，使得
对任意
都成立？若存在，求出λ；若不存在，请举出反例．
（3）若数列为“类等比数列”，且，
(a，b为常数)，求数列
的前n项之和
；数列
的前n项之和记为
，求
.
要制造一种机器零件，甲机床废品率为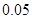
，而乙机床废品率为
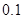，而它们
的生产是独立的，从它们制造的产品中，分别任意抽取一件，求：
（1）其中至少有一件废品的概率；（2）其中至多有一件废品的概率.
三个元件
正常工作的概率分别为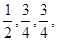
将它们中某两个元件并联后再和第三元件串联接入电路.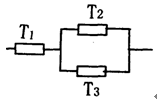
（Ⅰ）在如图的电路中，电路不发生故障的概率是多少？
（Ⅱ）三个元件连成怎样的电路，才能使电路中不发生故障的概率最大？请画出此时电路图，并说明理由.
如图，
两点之间有
条网线并联，它们能通过的最大信息量分别为
.现从中任取三条网线且使每条网线通过最大的信息量.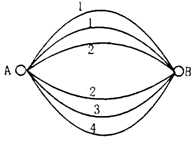
（I）设选取的三条网线由
到
可通过的信息总量为
，当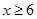
时，则保证信息畅通.求线路信息畅通的概率；
（II）求选取的三条网线可通过信息总量的数学期望.
某学生语、数、英三科考试成绩，在一次考试中排名全班第一的概率：语文为
，数学为
，英语为
，问一次考试中
（Ⅰ）三科成绩均未获得第一名的概率是多少？
（Ⅱ）恰有一科成绩未获得第一名的概率是多少
奖器有
个小球，其中
个小球上标有数字
，个小球上标有数字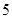
，现摇出
个小球，规定所得奖金（元）为这个小球上记号之和，求此次摇奖获得奖金数额的数学期望