本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分6分.
已知椭圆 过点
过点 ,两焦点为
,两焦点为 、
、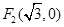 ,
, 是坐标原点,不经过原点的直线
是坐标原点,不经过原点的直线 与椭圆交于两不同点
与椭圆交于两不同点 、
、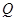 .
.
(1)求椭圆C的方程;
(2) 当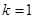 时,求
时,求 面积的最大值;
面积的最大值;
(3) 若直线 、
、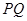 、
、 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线 的斜率
的斜率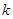 .
.
已知, 为圆
为圆 的直径,
的直径, 为垂直
为垂直 的一条弦,垂足为
的一条弦,垂足为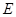 ,弦
,弦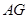 交
交 于
于 .
.
(1)求证: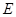 、
、 、
、 、
、 四点共圆;
四点共圆;
(2)若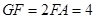 ,求线段
,求线段 的长.
的长. 
已知函数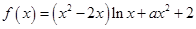 .
.
(1)当 时,求
时,求 在
在 处的切线方程;
处的切线方程;
(2)设函数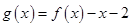 ,
,
(ⅰ)若函数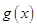 有且仅有一个零点时,求
有且仅有一个零点时,求 的值;
的值;
(ⅱ)在(ⅰ)的条件下,若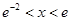 ,
,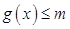 ,求
,求 的取值范围.
的取值范围.
已知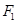 、
、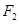 为椭圆
为椭圆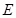 的左右焦点,点
的左右焦点,点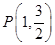 为其上一点,且有
为其上一点,且有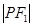
 .
.
(1)求椭圆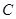 的标准方程;
的标准方程;
(2)过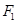 的直线
的直线 与椭圆
与椭圆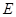 交于
交于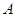 、
、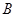 两点,过
两点,过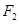 与
与 平行的直线
平行的直线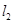 与椭圆
与椭圆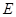 交于
交于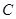 、
、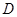 两点,求四边形
两点,求四边形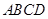 的面积
的面积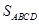 的最大值.
的最大值.
如下图,在三棱锥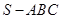 中,
中, 底面
底面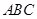 ,点
,点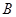 为以
为以 为直径的圆上任意一动点,且
为直径的圆上任意一动点,且 ,点
,点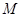 是
是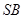 的中点,
的中点,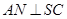 且交
且交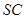 于点
于点 .
.
(1)求证: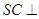 面
面 ;
;
(2)当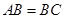 时,求二面角
时,求二面角 的余弦值.
的余弦值.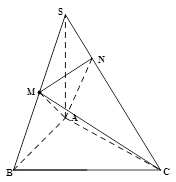
从天气网查询到邯郸历史天气统计(2011-01-01到2014-03-01)资料如下:
自2011-01-01到2014-03-01,邯郸共出现:多云 天,晴
天,晴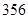 天,雨
天,雨 天,雪
天,雪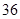 天,阴
天,阴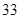 天,其它2天,合计天数为:
天,其它2天,合计天数为: 天.
天.
本市朱先生在雨雪天的情况下,分别以 的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为
的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为 元或
元或 元;在非雨雪天的情况下,他以
元;在非雨雪天的情况下,他以 的概率骑自行车上班,每天交通费用
的概率骑自行车上班,每天交通费用 元;另外以
元;另外以 的概率打出租上班,每天交通费用
的概率打出租上班,每天交通费用 元.(以频率代替概率,保留两位小数. 参考数据:
元.(以频率代替概率,保留两位小数. 参考数据: )
)
(1)求他某天打出租上班的概率;
(2)将他每天上班所需的费用记为 (单位:元),求
(单位:元),求 的分布列及数学期望.
的分布列及数学期望.