设 分别是椭圆
分别是椭圆 的 左,右焦点。
的 左,右焦点。
(1)若P是该椭圆上一个动点,求 的 最大值和最小值。
的 最大值和最小值。
(2)设过定点M(0,2)的 直线l与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l斜率k的取值范围。
已知椭圆C:的长轴长为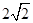 ,离心率
,离心率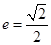 .
.
Ⅰ)求椭圆C的标准方程;
Ⅱ)若过点B(2,0)的直线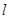 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且 OBE与
OBE与 OBF的面积之比为
OBF的面积之比为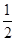 ,求直线
,求直线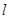 的方程.
的方程.
已知函 数 .
.
(1)若曲线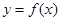 在点
在点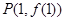 处的切线与直线
处的切线与直线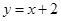 垂直,求函数
垂直,求函数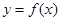 的单调区间;
的单调区间;
(2)若对于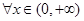 都有
都有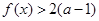 成立,试求
成立,试求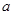 的取值范围;
的取值范围;
(3)记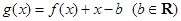 .当
.当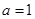 时,函数
时,函数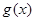 在区间
在区间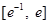 上有两个零点,求实数
上有两个零点,求实数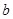 的取值范围.
的取值范围.
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B—PC—D的大小为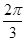 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为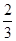 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(1)随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为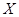 ,求
,求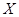 的分布列;
的分布列;
(3)随机选取3件产品,求这三件产品都不能通过检测的概率.
在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c = ,
,
(1)求角C的大小;
(2)求△ABC的面积.