一商场有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑，某中学准备从甲、乙两种品牌的电脑中各选购一种型号的电脑安装到各班教室．
（1）写出所有选购方案（利用树状图或列表法表示）；
（2）若（1）中各种选购方案被选中的可能性相同，那么A型号被选中的概率是多少？
（3）已知该中学用18万元人民币购买甲、乙两种品牌电脑刚好32台（价格如下表所示，单位：万元），其中甲品牌电脑选为A型号，求该中学购买到A型号电脑多少台？
| 品牌 |
甲 |
乙 |
|||
| 型号 |
A |
B |
C |
D |
E |
| 单价（万元） |
0．6 |
0．4 |
0．25 |
0．5 |
0．2 |
某特技飞行队在名胜风景旅游区——张家界天门洞特技表演， 其中一架飞机起飞后的高度变化如下表：（本题7分）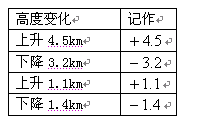
(1)此时这架飞机比起飞点高了多少千米？
(2)如果飞机每上升或下降1 km需消耗2L燃油，那么这架飞机在这4个动作表演过程中，一共消耗了多少升燃油？
(3)如果飞机做特技表演时，有4个规定动作，前3个动作起飞后高度变化如下：上升3.8km，下降2.9km，再上升1.6km,若要使飞机最终比起飞点高出1km，问第4个动作是上升还是下降，上升或下降多少千米？
已知：有10袋玉米，每袋玉米的标准重理是80千克，设超过的重量记为正，不足的重量记为负，统计的重量如下：(本题6分)
+1， +1， +1.5，－1， +1.2， +1.3，－1.3，－1.2， +1.8， +1.1
问：（1）与标准重量比较，10袋玉米总计超过多少千克？（2）10袋玉米的总重量是多少？
若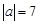
，
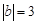，a,b同号。求a+b的值 (本题6分)
计算：(1) (－2)+(－3)；
(2)－4－4；
（3）
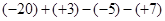
（4）
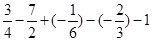
（5）6.1－3.7＋1.8－4.9
（6）（＋9）－（＋10）＋（－2）－（－8）＋3
在数轴上画出表示下列各数的点，并用“<”将各数连接起来．（本题4分）
，
，
，
，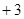