已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠ACB = ∠EDF = 90°，∠DEF = 45°，AC =" 8" cm，BC =" 6" cm，EF =" 9" cm。
如图（2），△DEF从图（1）的位置出发，以1 cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移。DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）。解答下列问题：
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由。
（3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由。（图（3）供同学们做题使用）
（1）计算：
；（2）化简：
．
解答一个问题后，将结论作为条件之一，提出与原问题有关的新问题，我们把它称为原问题的一个“逆向”问题．例如，原问题是“长方形的长和宽的长分别是3和4，求长方形的周长”，求出周长等于14后，它的一个“逆向”问题可以是“若长方形的周长为14，且一边长为3，求另一边的长”；也可以是“若长方形的周长为14，求长方形面积的最大值”，等等．
（1）设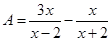
，
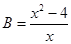，求A与B的积；
（2）提出（1）的一个“逆向”问题，并解答这个问题．
已知如图，AB∥CD∥EF，点M、N、P分别在AB、CD、EF上，NQ平分∠MNP．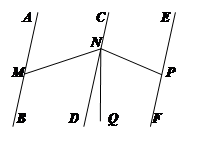
（1）若∠AMN＝50º，∠EPN＝70º，分别求∠MNP，∠DNQ的度数；
（2）若∠AMN＝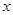
度，∠EPN＝
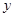度，请直接写出∠DNQ的度数（用含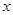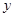，的代数式表示）；
（3）试探究：∠DNQ与∠AMN，∠EPN之间的数量关系，并说明理由．
下面是小明对多项式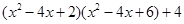
进行因式分解的过程．
解：设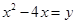
．
原式＝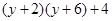
（第一步）
＝
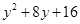（第二步）
＝
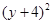（第三步）
＝
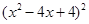（第四步）
回答下列问题：
（1）小明从第二步到第三步运用了因式分解的．
| A．提取公因式 | B．平方差公式 |
| C．两数和的完全平方公式 | D．两数差的完全平方公式 |
（2）小明因式分解的结果是否彻底？答：（填“彻底”或“不彻底”）；若不彻底，请直接写出因式分解的最后结果．
（3）请你模仿以上方法尝试对多项式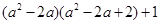
进行因式分解．
一家公司加工一批农产品，有粗加工和精加工两种方式．如果进行粗加工，每天可加工15吨；如果进行精加工，每天可加工5吨．该公司从市场上收购了农产品150吨，并用14天加工完这批农产品．根据题意，甲、乙两名同学分别列出的方程组(部分)如下：
甲：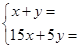
乙：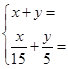
（1）根据甲、乙两名同学所列的方程组，请你在方框中补全甲、乙两名同学所列的方程组；
（2）求粗加工和精加工这批农产品各多少吨？