如图所示,质量均为m的物体B、C分别与轻质弹簧的两端相栓接,将它们放在倾角为θ的足够长的光滑斜面上,静止时弹簧的形变量为x0。斜面底端有固定挡板D,物体C靠在挡板D上。将质量也为m的物体A从斜面上的某点卣静止释放,A与B相碰。已知重力加速度为g,弹簧始终处于弹性限度内,不计空气阻力。
(1)若A与B相碰后粘连在一起做简谐运动,求AB通过平衡位置时弹簧的形变量;
(2)在(1)问中,当AB第一次振动到最高点时,C对挡板D的压力恰好为零,求振动过程C 对挡板D的压力最大值:
(3)若将A从距离B为9x0。的位置由静止释放,A与B相碰后不粘连,但仍立即一起运动,且当B第一次运动到最高点时,C对挡板D的压力也恰好为零。已知A与B相碰后,A、B系统动能损失一半,求A与B相碰后弹簧第一次恢复到原长时B的速度大小。
在一次军事演习中,解放军战士为了让炮弹以200m/s的速度击中前方450m高山崖上的某处军事目标,那大炮射击时至少需要让炮弹以多少的速度射出?
一位质量m=50kg的滑雪运动员从高度h=30m的斜坡自由滑下(初速度为零)。斜坡的倾角θ=37°,滑雪板与雪面滑动摩擦因素 =0.1。则运动员滑至坡底的过程中有:
=0.1。则运动员滑至坡底的过程中有:
(1)所受几个力所做的功各是多少?
(2)合力做了多少功?
(3)到达坡底时摩擦力的功率是多少?(不计空气阻力)
如图,一质量为5kg的滑块在F=15N的水平拉力作用下,由静止开始做匀加速直线运动,若滑块与水平地面间的动摩擦因数为0.2,g取10m/s2,问:滑块运动的加速度多大?滑块在力F作用下经5s通过的位移是多大?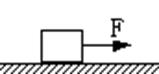
在水平路面上用绳子拉一只重110N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动,求箱子和地面间的动摩擦因数. (取sin370=0.6,cos370=0.8.)
火车通过桥梁、隧道的时候,要提前减速。一列以72km/h的速度行驶的火车在驶近一座石拱桥时作匀减速运动,减速行驶了2min,加速度大小为0.1m/s2,火车减速后的速度是多大?