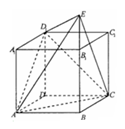
如图长方体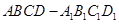 中,底面ABCD是边长为1的正方形,E为
中,底面ABCD是边长为1的正方形,E为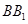 延长线上的一点且满足
延长线上的一点且满足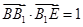 .
.
(1)求证: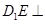 平面
平面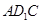 ;
;
(2)当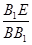 为何值时,二面角
为何值时,二面角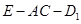 的大小为
的大小为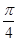 .
.
已知函数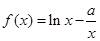 ,
,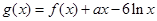 ,其中
,其中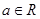 .
.
(Ⅰ)讨论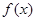 的单调性;
的单调性;
(Ⅱ)若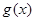 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数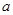 的取值范围;
的取值范围;
(Ⅲ)设函数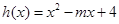 ,当
,当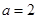 时,若
时,若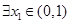 ,
,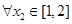 ,总有
,总有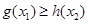 成立,求实数
成立,求实数 的取值范围.
的取值范围.
设 ,函数
,函数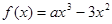 .
.
(1)若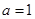 ,求函数
,求函数 的极值与单调区间;
的极值与单调区间;
(2)若函数 的图象在
的图象在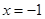 处的切线与直线
处的切线与直线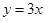 平行,求
平行,求 的值;
的值;
(3)若函数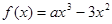 的图象与直线
的图象与直线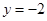 有三个公共点,求
有三个公共点,求 的取值范围.
的取值范围.
已知向量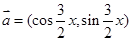 ,
, ,且
,且 .
.
(1)当 时,求
时,求 ;
;
(2)设函数 ,求函数
,求函数 的最值及相应的
的最值及相应的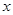 的值.
的值.
单调递增数列 的前
的前 项和为
项和为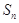 ,且满足
,且满足 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)数列 满足
满足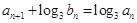 ,求数列
,求数列 的前
的前 项和
项和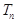 .
.
已知函数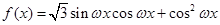 的周期为
的周期为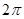 ,其中
,其中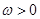 .
.
(Ⅰ)求 的值及函数
的值及函数 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,设内角A、B、C所对边的长分别为a、b、c,若
中,设内角A、B、C所对边的长分别为a、b、c,若 ,
, ,f(A)=
,f(A)= ,求b的值.
,求b的值.