已知椭圆C：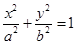
( 
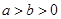)的离心率为
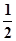，点(1，
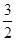)在椭圆C上.
（1）求椭圆C的方程；
（2）若椭圆C的两条切线交于点M(4，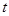
)，其中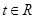
，切点分别是A、B，试利用结论：在椭圆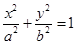上的点(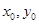
)处的椭圆切线方程是
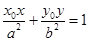，证明直线AB恒过椭圆的右焦点
；
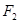（3）试探究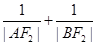
的值是否恒为常数，若是，求出此常数；若不是，请说明理由.
设函数
定义域为
．
（1）若
，求实数
的取值范围；
（2）若
在
上恒成立，求实数的取值范围．
销售甲、乙两种商品所得利润分别为P（单位：万元）和Q（单位：万元），它们与投入资金
（单位：万元）的关系有经验公式
, 
.今将3万元资金投入经营甲、乙两种商品，其中对甲种商品投资
（单位：万元）
（1）试建立总利润
（单位：万元）关于的函数关系式，并指明函数定义域；
（2）如何投资经营甲、乙两种商品，才能使得总利润最大.
（本小题满分14分）
先解答（1），再通过结构类比解答（2）：
（1）请用tanx表示
，并写出函数
的最小正周期；
（2）设
为非零常数，且
，试问
是周期函数吗？证明你的结论.
已知函数
（1）判定并证明函数的奇偶性；
（2）试证明
在定义域内恒成立；
（3）当
时，
恒成立，求m的取值范围.
已知复数
，(其中
为虚数单位)
（1）当复数
是纯虚数时，求实数
的值；
（2）若复数对应的点在第三象限，求实数的取值范围.