下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“ ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
空气质量指数( ) ) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
“ ” ” 小时平均浓度( 小时平均浓度( ) ) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘ ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率;
发生的概率;
(3)在上表数据中,在表示空气质量优良的日期中,随机抽取 天,记
天,记 为“
为“ ”
” 小时平均浓度不超过
小时平均浓度不超过 的天数,求
的天数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.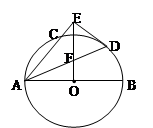
(1)求证:DE是⊙O的切线;
(2)若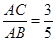 ,求
,求 的值.
的值.
(本小题满分12分)已知数列 各项均不为0,其前
各项均不为0,其前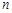 项和为
项和为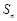 ,且对任意
,且对任意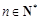 都有
都有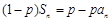 (
(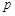 为大于1的常数),记
为大于1的常数),记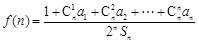 .
.
(1) 求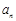 ;
;
(2) 试比较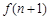 与
与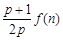 的大小(
的大小(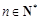 );
);
(3) 求证:
(本小题满分12分)己知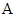 、
、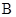 、
、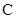 是椭圆
是椭圆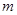 :
: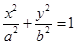 (
(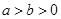 )上的三点,其中点
)上的三点,其中点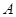 的坐标为
的坐标为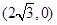 ,
,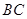 过椭圆的中心,且
过椭圆的中心,且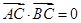 ,
,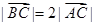 。
。
(Ⅰ)求椭圆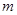 的方程;
的方程;
(Ⅱ)过点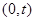 的直线
的直线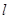 (斜率存在时)与椭圆
(斜率存在时)与椭圆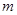 交于两点
交于两点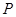 ,
,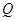 ,设
,设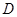 为椭圆
为椭圆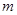 与
与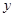 轴负半轴的交点,且
轴负半轴的交点,且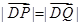 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知f(x)=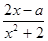 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=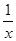 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
(本小题满分12分) 已知一个四棱锥的三视图如图所示,其中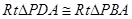 ,且
,且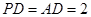 ,
,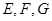 分别为
分别为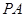 、
、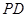 、
、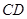 的中点
的中点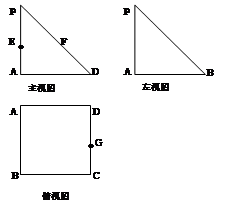
(1)求证:PB//平面EFG
(2)求直线PA与平面EFG所成角的大小
(3)在直线CD上是否存在一点Q,使二面角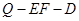 的大小为
的大小为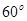 ?若存在,求出CQ的长;若不存在,请说明理由。
?若存在,求出CQ的长;若不存在,请说明理由。