(本小题满分12分)为了响应国家号召,某地决定分批建设保障性住房供给社会.首批计划用100万元购得一块土地,该土地可以建造每层1 000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高20元.已知建筑第5层楼房时,每平方米建筑费用为800元.
(1)若建筑第x层楼时,该楼房综合费用为y万元(综合费用是建筑费用与购地费用之和),写出y=f(x)的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,应把楼层建成几层?此时平均综合费用为每平方米多少元?
(本小题满分12分)已知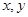 都是正数.
都是正数.
(1)若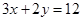 ,求
,求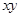 的最大值;
的最大值;
(2)若 ,求
,求 的最小值.
的最小值.
(本小题满分10分)解下列不等式
(Ⅰ)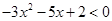
(Ⅱ)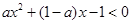
已知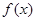 是定义在
是定义在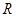 上的函数,对任意的
上的函数,对任意的 ,
,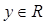 都有
都有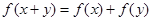 ,且
,且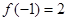
(1)求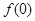 ,
,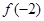 的值;
的值;
(2)证明:函数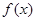 在
在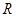 上是奇函数.
上是奇函数.
已知 是定义在
是定义在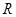 上的偶函数,且
上的偶函数,且 时,
时,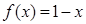
(1)求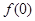 ,
,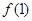 的值;
的值;
(2)求 的解析式.
的解析式.